PROBLEMA No. 4
TECNICO MANTENIMIENTO AERONAUTICO :: Auxiliar :: MOMENTOS Y REACCIONES EN VIGAS Y ESTRUCTURAS_080608
Página 1 de 2.
Página 1 de 2. • 1, 2 
Admin- Admin
- Cantidad de envíos : 450
Fecha de inscripción : 14/03/2008 -
JOSE MELENDEZ
mr060909 Dom 08 Jun 2008, 11:19
ING ,YO EN MI CASO SE ME DIFICULTA BASTANTE HACER LOS EJERCICIOS, A ESO LE AGREGO Q TIEMPO NO TENGO PORQUE ENTRO A TRABAJAR A LAS 12 ESTE DUDO Q LO PUEDA HACER ME RETIRO Y MI GRAN TRABAJO ESPERO TOME EN CUNETA LO Q LE MENCIONO GRACIAS.
DESEARIA QUE PUSIERA MAS EJERCICIOS EN CLASE Y NO SOLAMENTE EN EL FORO YA QUE A ALGUNOS DE NOSOTROS SE NOS DIFICULTA EL ENTENDIMIENTO DE LOS EJERCICIOS
POR CIERTO YA VOY TARDE PA EL TRABAJO
GRACIAS.
Q TENGA UN BUEN DIA.
DESEARIA QUE PUSIERA MAS EJERCICIOS EN CLASE Y NO SOLAMENTE EN EL FORO YA QUE A ALGUNOS DE NOSOTROS SE NOS DIFICULTA EL ENTENDIMIENTO DE LOS EJERCICIOS
POR CIERTO YA VOY TARDE PA EL TRABAJO
GRACIAS.
Q TENGA UN BUEN DIA.
mr060909- Invitado
Gaspar Perez
PM-04012 Dom 08 Jun 2008, 11:42
Hey gente, No COPIEN
Piensen un rato, que para el parcial no va ver Foro para comparar.
Piensen un rato, que para el parcial no va ver Foro para comparar.
PM-04012- Invitado
problema 4
vicente Dom 08 Jun 2008, 11:46
hey profe no entiendo no puedo hacer ete problema !!!!!!! ya me abati ya vere como diablos lo hago
vicente- Invitado
Respuesta 4
Gv070869 Dom 08 Jun 2008, 11:46
Jose Enrique García Villalta (kike)
respuesta 4
Ing, este es lo que yo entendi y que pude desarrollar del ejercicio 4 :
Lo realice con vectores unitarios.
tenemos que...:
Fa= (-1.4i+1.4j-0.7/2.1) lo mismo para Fb
FA=FB(0.67i+067j-0.33i)
sumatoria en fuerzas en x=0 sumatoria de fuerzas en y =0
0.67FB+0.67FA=0
-0.67FA+0.67FB=0
FA=FB
sumatoria de fuerzas en Z=0
2.2KN-(0.7FB)^2=0
FB= 1.57KN
FA= 1.57KN.....
respuesta 4
Ing, este es lo que yo entendi y que pude desarrollar del ejercicio 4 :
Lo realice con vectores unitarios.
tenemos que...:
Fa= (-1.4i+1.4j-0.7/2.1) lo mismo para Fb
FA=FB(0.67i+067j-0.33i)
sumatoria en fuerzas en x=0 sumatoria de fuerzas en y =0
0.67FB+0.67FA=0
-0.67FA+0.67FB=0
FA=FB
sumatoria de fuerzas en Z=0
2.2KN-(0.7FB)^2=0
FB= 1.57KN
FA= 1.57KN.....
Gv070869- Invitado
Re: PROBLEMA No. 4
cc080745 Dom 08 Jun 2008, 11:48
hey ingeniero tengo que desconectarme y no entiendo el ultimo ejercicio pero voy a ver si lo puedo hacr
cc080745- Invitado
Re: PROBLEMA No. 4
vicente Dom 08 Jun 2008, 12:06
hey prfe le voy a mandar este ejercicio acorreo y se lo voy a entregar impreso mañana porque no lo entiendo le voy a preguntar a alguien que lo haya hecho para que me explique porque ya me teno que desconectar gracias........vicente gochez......gl080803
vicente- Invitado
MARIO TRUJILLO
TM080812 Dom 08 Jun 2008, 12:34
ING. JOAQUÍN:YO TENGO QUE VIAJAR PARA SAN SALVADOR A LA 1 p.m. YA QUE NO POSEO VEHICULO PROPIO Y VIAJARE CON UN FAMILIAR Y DISPONGO DEL TIEMPO DE ELLOS Y NO DE MI TIEMPO Y ELLOS PARTIRAN A LA 1... POR LO QUE SI SE PERMITE MANDARE LA RESOLUCION DEL EJERCICIO 4 A SU CORREO.
POR SU ATTE.
GRACIAS.
TM080812- Invitado
Dificultades...............
AE060644 Dom 08 Jun 2008, 13:08
Ingeniero, creo que este ultimo dificilmente lo resolveria, el problema es que tenia compromiso a la 1pm y me tenia que haber ido a las 12.30 de aqui (pensando q solo eran 2 problemas)........
la cuestion es que creo que este ultimo si no lo puedo sacar pues ne han venido a traer y no puedo hacerlos esperar, creo que me voy a aventurar solo con los tres que respondi xq este si esta "candela"..........
espero de su comprension y nos vemos mañana "bien afilado" para el parcial, se cuida y que pase un feliz dia tambien...
Alvaro Roberto Ambrogi Escobar
la cuestion es que creo que este ultimo si no lo puedo sacar pues ne han venido a traer y no puedo hacerlos esperar, creo que me voy a aventurar solo con los tres que respondi xq este si esta "candela"..........
espero de su comprension y nos vemos mañana "bien afilado" para el parcial, se cuida y que pase un feliz dia tambien...
Alvaro Roberto Ambrogi Escobar
AE060644- Invitado
Julio cesar Rodriguez Barbero
RB080774 Dom 08 Jun 2008, 14:07
Ultima respuesta pero no se si esta buena, porque tengo unas dudas, por si acaso sirve aca la dejo
Primero debemos encontrar las tensiones TCA, TCB es necesario la direccion de los vectores CA, CB, después encontrar el vector unitario que nos dara la dirección para multiplicar por la magnitud máxima de fuerza que resisten
CA = - (1.4m)i + (1.4m)j – (0.7m)k
= 2.1m
λCA = - (1.4m)i + (1.4m)j – (0.7m)k / (2.1m)
λCA = - (0.67m)i + (0.67m)j- (0.33m)k
CB = (1.4m)i + (1.4m)j- (0.7m)k
= 2.1m
λCB = (1.4m)i + (1.4m)j- (0.7m)k / ( 2.1m)
λCB = (0.67m)i + (0.67m)j- (0.33m)k
Para cada cable la fuerza máxima es de 2.2KN entonces tenemos la dirección y multiplicamos esta fuerza máxima por la dirección, teniendo asi:
λCA x (fuerza maxima) = (- (0.67m)i + (0.67m)j- (0.33m)k) (2.2KN)
TCA = -1474Ni + 1474Nj – 726Nk
λCB x (fuerza máxima) = ((0.67m)i + (0.67m)j- (0.33m)k) (2.2KN)
TCB = 1474Ni + 1474Nj – 726Nk
∑F = 0
∑ F = TCB + TCA + F = 0
∑Fz = 0
-726Nk – 726Nk +Fk = 0
(726N+726N)k / k = F
1452N = F
Esta es la fuerza máxima que puede aguantar los cables que la sostienen, que es de 1.452KN
La reaccion en el punto E no la coloco porque segun el analisis que hice me da cero, entonces no habria reaccion de ese punto si lo analizo con respecto a la direccion de la fuerza del viento.
Primero debemos encontrar las tensiones TCA, TCB es necesario la direccion de los vectores CA, CB, después encontrar el vector unitario que nos dara la dirección para multiplicar por la magnitud máxima de fuerza que resisten
CA = - (1.4m)i + (1.4m)j – (0.7m)k
= 2.1m
λCA = - (1.4m)i + (1.4m)j – (0.7m)k / (2.1m)
λCA = - (0.67m)i + (0.67m)j- (0.33m)k
CB = (1.4m)i + (1.4m)j- (0.7m)k
= 2.1m
λCB = (1.4m)i + (1.4m)j- (0.7m)k / ( 2.1m)
λCB = (0.67m)i + (0.67m)j- (0.33m)k
Para cada cable la fuerza máxima es de 2.2KN entonces tenemos la dirección y multiplicamos esta fuerza máxima por la dirección, teniendo asi:
λCA x (fuerza maxima) = (- (0.67m)i + (0.67m)j- (0.33m)k) (2.2KN)
TCA = -1474Ni + 1474Nj – 726Nk
λCB x (fuerza máxima) = ((0.67m)i + (0.67m)j- (0.33m)k) (2.2KN)
TCB = 1474Ni + 1474Nj – 726Nk
∑F = 0
∑ F = TCB + TCA + F = 0
∑Fz = 0
-726Nk – 726Nk +Fk = 0
(726N+726N)k / k = F
1452N = F
Esta es la fuerza máxima que puede aguantar los cables que la sostienen, que es de 1.452KN
La reaccion en el punto E no la coloco porque segun el analisis que hice me da cero, entonces no habria reaccion de ese punto si lo analizo con respecto a la direccion de la fuerza del viento.
RB080774- Invitado
Re: PROBLEMA No. 4
oscar Dom 08 Jun 2008, 14:33
OSCAR ALEXANDER MAURICIO NAJERA MN080822
PROBLEMA N.3
En este ejercicio comenzamos primero por encontrar los vectores unitarios de los vectores CA y BC
CA = - 1.4mi + 1.4mj – 0.7mk CA= 2.1m
λCA = CA/CA
λCA = - 0.67mi + 0.67mj- 0.33mk
CB = 1.4mi + 1.4mj- 0.7mk
λCB = CB/CB
λCB = 0.67mi + 0.67mj- 0.33mk
Nos dicen en el problema q cada cable debe resistir una carga axial de 2.2kN entonces:
λCA x ( 2.2kN) = (- 0.67mi + 0.67mj- 0.33mk) (2.2KN)
TCA = -1474Ni + 1474Nj – 726Nk
λCB x ( 2.2 kN) = (0.67mi + 0.67mj- (0.33mk) (2.2KN)
TCB = 1474Ni + 1474Nj – 726Nk
∑F = 0
∑ F = TCB + TCA + F = 0
∑Fz = 0
-726Nk – 726Nk +Fk = 0
(726N+726N)k / k = F
1452N = F
PROBLEMA N.3
En este ejercicio comenzamos primero por encontrar los vectores unitarios de los vectores CA y BC
CA = - 1.4mi + 1.4mj – 0.7mk CA= 2.1m
λCA = CA/CA
λCA = - 0.67mi + 0.67mj- 0.33mk
CB = 1.4mi + 1.4mj- 0.7mk
λCB = CB/CB
λCB = 0.67mi + 0.67mj- 0.33mk
Nos dicen en el problema q cada cable debe resistir una carga axial de 2.2kN entonces:
λCA x ( 2.2kN) = (- 0.67mi + 0.67mj- 0.33mk) (2.2KN)
TCA = -1474Ni + 1474Nj – 726Nk
λCB x ( 2.2 kN) = (0.67mi + 0.67mj- (0.33mk) (2.2KN)
TCB = 1474Ni + 1474Nj – 726Nk
∑F = 0
∑ F = TCB + TCA + F = 0
∑Fz = 0
-726Nk – 726Nk +Fk = 0
(726N+726N)k / k = F
1452N = F
oscar- Invitado
OCTAVIO AMAYA
AA070857 Dom 08 Jun 2008, 14:50
DANIEL OCTAVIO AMAYA ARÁUZ AA070857
RESOLUCION PROBLEMA #4
/A/ = (1.4m)i + (1.4)j + (0.7)k = 0
/B/ = 2.8(i) + (-1.4)j + (0.7)k = 0
/C/ = 2.8(i) + (1.4)j + 0k = 0
ΣFx = 2.8(i) + (1.4)i + 2.8(i)
ΣFx = 7i
ΣFy = 1.4j
ΣFz = 0.7k + 0.7k + 2.2KNk
ΣFz = 1.4mk + 2.2KNk
R = √(7)² + (1.4)² + (1.4)²
R = √52.92
R = 7.27m
ΣM = 0
(2.2KN)(0.7m) = 0
ΣM=(1540 KN ∙m)/(7.27 m)
ΣM = 678.41 KN
RESOLUCION PROBLEMA #4
/A/ = (1.4m)i + (1.4)j + (0.7)k = 0
/B/ = 2.8(i) + (-1.4)j + (0.7)k = 0
/C/ = 2.8(i) + (1.4)j + 0k = 0
ΣFx = 2.8(i) + (1.4)i + 2.8(i)
ΣFx = 7i
ΣFy = 1.4j
ΣFz = 0.7k + 0.7k + 2.2KNk
ΣFz = 1.4mk + 2.2KNk
R = √(7)² + (1.4)² + (1.4)²
R = √52.92
R = 7.27m
ΣM = 0
(2.2KN)(0.7m) = 0
ΣM=(1540 KN ∙m)/(7.27 m)
ΣM = 678.41 KN
AA070857- Invitado
CARLOS AMAYA
AA080754 Dom 08 Jun 2008, 14:58
RESPUESTA AL EJERCICIO #3
A+B-1000=0
A+B=1000 lb
-A(20cos10)+ 1000 lb (8ft)= 0
A=(-8000 lb/ft)/(-20cos10 ft)
A=406.17 lb
B=1000 lb-406.17 lb
B=593.89 lb
A+B-1000=0
A+B=1000 lb
-A(20cos10)+ 1000 lb (8ft)= 0
A=(-8000 lb/ft)/(-20cos10 ft)
A=406.17 lb
B=1000 lb-406.17 lb
B=593.89 lb
AA080754- Invitado
Respuesta 4
AH030408 Dom 08 Jun 2008, 14:59
Luis Mario Abrego Hernández
Tanto el vector CA y el CB son iguales
Tenemos que CA = CB
CA = √((1.4) ² + (1.4) ²+(0.7)²) = 2.1
FCA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = -1.47i + 1.47j – 0.73k
FCB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = 1.47i + 1.47j – 0.73k
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
Despejamos:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
Sumatoria de momentos en D
∑FD = ∑(rxf)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Por el método de determinante resolvemos los productos vectoriales:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058k + 2.058k) + (2.
(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Agrupando:
(-1.022 + 0.7 P – 1.029)i + (-1.4P + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
De lo anterior obtenemos 3 ecuaciones:
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4P + 2.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Encontrando el P: de la Ec. 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
La maxima fuerza del viento permitida
P = 2.93 kN
Encontrando Ez de la ecuación 2
-1.4P + 2.058 – 2.8Ez = 0
-1.4(2.93) + 2.058 – 2.8Ez = 0
-4.102 +2.058 – 2.8Ez = 0
-2.102 – 2.8Ez = 0
– 2.8Ez = 2.102
Componente z de la reacción E
Ez = - 0.75 kN
Tanto el vector CA y el CB son iguales
Tenemos que CA = CB
CA = √((1.4) ² + (1.4) ²+(0.7)²) = 2.1
FCA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = -1.47i + 1.47j – 0.73k
FCB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = 1.47i + 1.47j – 0.73k
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
Despejamos:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
Sumatoria de momentos en D
∑FD = ∑(rxf)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Por el método de determinante resolvemos los productos vectoriales:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058k + 2.058k) + (2.
(Eyk –Ezj) = 0-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Agrupando:
(-1.022 + 0.7 P – 1.029)i + (-1.4P + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
De lo anterior obtenemos 3 ecuaciones:
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4P + 2.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Encontrando el P: de la Ec. 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
La maxima fuerza del viento permitida
P = 2.93 kN
Encontrando Ez de la ecuación 2
-1.4P + 2.058 – 2.8Ez = 0
-1.4(2.93) + 2.058 – 2.8Ez = 0
-4.102 +2.058 – 2.8Ez = 0
-2.102 – 2.8Ez = 0
– 2.8Ez = 2.102
Componente z de la reacción E
Ez = - 0.75 kN
AH030408- Invitado
CARLOS AMAYA
AA080754 Dom 08 Jun 2008, 15:03
RESPUESTA #4
/A/ = (1.4m)i + (1.4)j + (0.7)k = 0
/B/ = (2.8)i + (-1.4)j + (0.7)k = 0
/C/ = (2.8)i + (1.4)j + 0k = 0
��Fx = (2.8)i + (1.4)i + (2.8)i
��Fx = 7i
��Fy = 1.4j
��Fz = 0.7k + 0.7k + 2.2KNk
��Fz = 1.4mk + 2.2KNk
R = √(7)² + (1.4)² + (1.4)²
R = √52.92
R = 7.27m
��M = 0
(2.2KN)(0.7m) = 0
ΣM=(1540 KN ∙m)/(7.27 m)
��M = 678.41 KN
/A/ = (1.4m)i + (1.4)j + (0.7)k = 0
/B/ = (2.8)i + (-1.4)j + (0.7)k = 0
/C/ = (2.8)i + (1.4)j + 0k = 0
��Fx = (2.8)i + (1.4)i + (2.8)i
��Fx = 7i
��Fy = 1.4j
��Fz = 0.7k + 0.7k + 2.2KNk
��Fz = 1.4mk + 2.2KNk
R = √(7)² + (1.4)² + (1.4)²
R = √52.92
R = 7.27m
��M = 0
(2.2KN)(0.7m) = 0
ΣM=(1540 KN ∙m)/(7.27 m)
��M = 678.41 KN
AA080754- Invitado
Oscar Merino
MC080736 Dom 08 Jun 2008, 15:03
primero sacamos los vectores
A= (1.4m)i + (1.4)j + (0.7)k = 0
B = 2.8(i) + (-1.4)j + (0.7)k = 0
C = 2.8(i) + (1.4)j + 0k = 0
luego hacemos sumatoria de fuerzas en x y z
Σx = 2.8(i) + (1.4)i + 2.8(i)
Σx = 7i
Σy = 1.4j
Σz = 0.7k + 0.7k + 2.2KNk
Σz = 1.4mk + 2.2KNk
luego sacamos la resultante
R = √(7)² + (1.4)² + (1.4)²
R = √52.92
R = 7.27m
y por ultimo hacmos una sumatoria de momentos.
ΣM = 0
(2.2KN)(0.7m) = 0
ΣM=(1540 KN ∙m)/(7.27 m)
ΣM = 678.41 KN
A= (1.4m)i + (1.4)j + (0.7)k = 0
B = 2.8(i) + (-1.4)j + (0.7)k = 0
C = 2.8(i) + (1.4)j + 0k = 0
luego hacemos sumatoria de fuerzas en x y z
Σx = 2.8(i) + (1.4)i + 2.8(i)
Σx = 7i
Σy = 1.4j
Σz = 0.7k + 0.7k + 2.2KNk
Σz = 1.4mk + 2.2KNk
luego sacamos la resultante
R = √(7)² + (1.4)² + (1.4)²
R = √52.92
R = 7.27m
y por ultimo hacmos una sumatoria de momentos.
ΣM = 0
(2.2KN)(0.7m) = 0
ΣM=(1540 KN ∙m)/(7.27 m)
ΣM = 678.41 KN
MC080736- Invitado
RESPUESTA TRES !!!!!!!
TR080758 Dom 08 Jun 2008, 15:04
BUENO CREO QUE MAS VALIA INTENTARLO PERO BUENO AHI VA :
JORGE ALBERTO TEOS RIVERA
TR080758
hijole!!!!! Esto esta cañon mire maestro yo no se si esta correcto pero la intención es lo q cuenta
PROBLEMA TRES!!!!!!!!!
Para empezar este bello ejercicio debemos encontrar los vectores unitarios donde tenemos:
Ca= --1.4i +1.4 j -- 0.7k
Aplicamos el teorema de Pitágoras
Ca= √(--1.4)^2+(1.4)^2+(--0.7)^2
Ca= 2.1m
Ahora ese resultado lo dividimos entre cada vector unitario así:
Ca= --1.4mi+1.4mj--0.7mk=2.1m
Ca= (1.4mi/2.1m) +(1.4mj/2.1m)--(0.7mk/2.1m)
Ca= 0.66mi+0.66mj--0.33mk
Ahora obtenemos el resultado para CB
Cb= 1.4mi+1.4mj-0.7mk
Cb= √(1.4)^2+(1.4)^2+(--0.7)^2
Cb= 2.1m
Dividimos también ese resultado entre todos los vectores unitarios y obtenemos:
Cb= (1.4mi)/2.1m)+(1.4mj/2.1m)-(0.7mk/2.1m)
Cb= 0.66mi+0.66mj+0.33mk
Los cables deben resistir una carga de 2.2Kn entonces tenemos un producto de un vector por un escalar asi:
Ca x 2.2kn= (-0.66i+0.66j-0.33k)(2.2kn)
Ca x 2.2kn= -1474Ni + 1474Nj – 726Nk
Cb x 2.2kn= (0.66i+0.66j+0.33k)(2.2kn)
Cb x2.2kn= 1474i+1474j-726k
Obtenemos la sumatoria de fuerzas para el caso y tenemos lo siguiente :
∑F = 0
∑F= Ca+Cb+P
∑Fz = 0
-726Nk – 726Nk +Pk = 0
(726N+726N)k / k = P
1452N = P
JORGE ALBERTO TEOS RIVERA
TR080758
hijole!!!!! Esto esta cañon mire maestro yo no se si esta correcto pero la intención es lo q cuenta
PROBLEMA TRES!!!!!!!!!
Para empezar este bello ejercicio debemos encontrar los vectores unitarios donde tenemos:
Ca= --1.4i +1.4 j -- 0.7k
Aplicamos el teorema de Pitágoras
Ca= √(--1.4)^2+(1.4)^2+(--0.7)^2
Ca= 2.1m
Ahora ese resultado lo dividimos entre cada vector unitario así:
Ca= --1.4mi+1.4mj--0.7mk=2.1m
Ca= (1.4mi/2.1m) +(1.4mj/2.1m)--(0.7mk/2.1m)
Ca= 0.66mi+0.66mj--0.33mk
Ahora obtenemos el resultado para CB
Cb= 1.4mi+1.4mj-0.7mk
Cb= √(1.4)^2+(1.4)^2+(--0.7)^2
Cb= 2.1m
Dividimos también ese resultado entre todos los vectores unitarios y obtenemos:
Cb= (1.4mi)/2.1m)+(1.4mj/2.1m)-(0.7mk/2.1m)
Cb= 0.66mi+0.66mj+0.33mk
Los cables deben resistir una carga de 2.2Kn entonces tenemos un producto de un vector por un escalar asi:
Ca x 2.2kn= (-0.66i+0.66j-0.33k)(2.2kn)
Ca x 2.2kn= -1474Ni + 1474Nj – 726Nk
Cb x 2.2kn= (0.66i+0.66j+0.33k)(2.2kn)
Cb x2.2kn= 1474i+1474j-726k
Obtenemos la sumatoria de fuerzas para el caso y tenemos lo siguiente :
∑F = 0
∑F= Ca+Cb+P
∑Fz = 0
-726Nk – 726Nk +Pk = 0
(726N+726N)k / k = P
1452N = P
TR080758- Invitado
respuesta 4
GR040641 Dom 08 Jun 2008, 15:14
Jaime OMar Guzman Ramirez
Tenemos los vectores CA y CB que son iguales:
Entonces CA = CB
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA=√4.41= 2.1
Buscando fuerzas de CA y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
Entonces:
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
Despejando:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
Sumando los momentos en “D”
∑FD = ∑(r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Resolviendo por producto vectorial:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Agrupamos:
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Entonces se obtienen 3 ecuaciones:
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Buscando P en Ec. 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
buscando Ez en Ec. 2
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Tenemos los vectores CA y CB que son iguales:
Entonces CA = CB
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA=√4.41= 2.1
Buscando fuerzas de CA y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
Entonces:
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
Despejando:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
Sumando los momentos en “D”
∑FD = ∑(r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Resolviendo por producto vectorial:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.
(Eyk –Ezj) = 0-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Agrupamos:
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Entonces se obtienen 3 ecuaciones:
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Buscando P en Ec. 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
buscando Ez en Ec. 2
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
GR040641- Invitado
Jose Mata
mm080805 Dom 08 Jun 2008, 15:48
bueno aqui va mi ultimo ejercicio al igual que los anteriores se lo envio por imagenes espero que no le moleste que se lo envie de esta forma, si no le parece que esta forma es correcta notificarmelo para que a futuro mis respuestas se las envie solamente en forma digital, de antmano muchas gracias.
la respuesta es: el valor maximo aceptable de la fuerza del viento es de 2.932kN
aqui estan los link:
https://i.servimg.com/u/f42/12/42/70/59/00110.jpg
https://i.servimg.com/u/f42/12/42/70/59/00210.jpg
https://i.servimg.com/u/f42/12/42/70/59/00310.jpg
https://i.servimg.com/u/f42/12/42/70/59/00510.jpg
primero obtenemos el diagrama de cuerpo libre, y tomamos el valor de 2.2kN para ambos soportes de madera, que es la fuerza maxima de tencion que pueden soportar, y buscamos el valor de la fuerza del viento P:
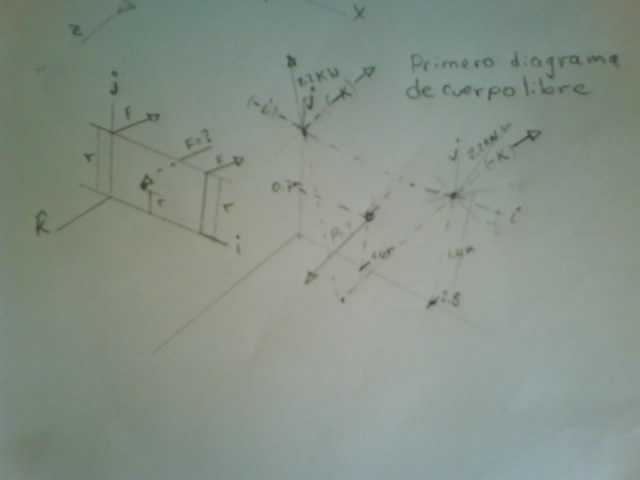
luego buscamos la herramienta fisica de torque o momento y buscamos los componentes rectangulares:
luego de obtener los componetes unitarios se obtiene la fuerza en componentes unitarios y se efectua lo mismo en la otra fuerza:
luego ordenamos los datos con los torques que necesitamos, como la hoja de plywood esta sostenida n su base lunica componete que hace torque es la componte z asi que usamos solo las componetes en K y sus respetivos brazos que serian desde el eje X perpendicularmnte al punto donde se aplicala fuerza:
solo resta substituir los valores de fuerza y brazo n la formula de equilibrio para obtener la fuerza P que es la fuerza del viento cuando los soportes de madera sufren una tensión de 2.2kN:
la respuesta es: el valor maximo aceptable de la fuerza del viento es de 2.932kN
aqui estan los link:
https://i.servimg.com/u/f42/12/42/70/59/00110.jpg
https://i.servimg.com/u/f42/12/42/70/59/00210.jpg
https://i.servimg.com/u/f42/12/42/70/59/00310.jpg
https://i.servimg.com/u/f42/12/42/70/59/00510.jpg
primero obtenemos el diagrama de cuerpo libre, y tomamos el valor de 2.2kN para ambos soportes de madera, que es la fuerza maxima de tencion que pueden soportar, y buscamos el valor de la fuerza del viento P:
luego buscamos la herramienta fisica de torque o momento y buscamos los componentes rectangulares:
luego de obtener los componetes unitarios se obtiene la fuerza en componentes unitarios y se efectua lo mismo en la otra fuerza:
luego ordenamos los datos con los torques que necesitamos, como la hoja de plywood esta sostenida n su base lunica componete que hace torque es la componte z asi que usamos solo las componetes en K y sus respetivos brazos que serian desde el eje X perpendicularmnte al punto donde se aplicala fuerza:
solo resta substituir los valores de fuerza y brazo n la formula de equilibrio para obtener la fuerza P que es la fuerza del viento cuando los soportes de madera sufren una tensión de 2.2kN:
mm080805- Invitado
Gaspar Perez
PM-04012 Dom 08 Jun 2008, 15:54
Gaspar Perez
Los vectores CA = CB
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA = √4.41= 2.1
CA = 2.1
CB = 2.1
Buscado los vectores unitarios CA y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
La Sumatorias de fuerza
F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
Entonces se tiene:
Fx =
Dx + Ex – 1.47 + 1.47 = 0
Dx + Ex = 0
Fy =
Dy + Ey + 1.47 +1.47 = 0
Dy + Ey = -2.94
Fz = Dz + Ez – 0.73 -0.73 + P= 0
Dz + Ez = 1.46 – P
Sumatoria de momentos en D
FD = (r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Producto vectorial:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Entonces tiene 3 ecuaciones:
Ec. 1: Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: Mz = 2.058 + 2.058 + 2.8Ey = 0
Encontrando P en Ecuacion 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
Encontrando Ez en Ecuacion 2
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Encontrando Ey de ecuacion 3
2.058 + 2.058 + 2.8Ey = 0
2.8Ey = -2.058-2.058
2.8Ey = -4.66
Ey = 1.66 kN
Los vectores CA = CB
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA = √4.41= 2.1
CA = 2.1
CB = 2.1
Buscado los vectores unitarios CA y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
La Sumatorias de fuerza
F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
Entonces se tiene:
Fx =
Dx + Ex – 1.47 + 1.47 = 0
Dx + Ex = 0
Fy =
Dy + Ey + 1.47 +1.47 = 0
Dy + Ey = -2.94
Fz = Dz + Ez – 0.73 -0.73 + P= 0
Dz + Ez = 1.46 – P
Sumatoria de momentos en D
FD = (r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Producto vectorial:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Entonces tiene 3 ecuaciones:
Ec. 1: Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: Mz = 2.058 + 2.058 + 2.8Ey = 0
Encontrando P en Ecuacion 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
Encontrando Ez en Ecuacion 2
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Encontrando Ey de ecuacion 3
2.058 + 2.058 + 2.8Ey = 0
2.8Ey = -2.058-2.058
2.8Ey = -4.66
Ey = 1.66 kN
PM-04012- Invitado
Carlos Enrique Rodríguez Lardé
RL081194 Dom 08 Jun 2008, 15:58
Tenemos que CA = CB
CA = √((1.4) ² + (1.4) ²+(0.7)²) = 2.1
FCA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = -1.47i + 1.47j – 0.73k
FCB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = 1.47i + 1.47j – 0.73k
∑F = 0
(Dx + Ex – 1.47 + 1.47 )i + (Dy + Ey + 1.47 +1.47 )j + (Dz + Ez – 0.73 -0.73 + P )k = 0
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
Despejamos:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
∑FD = ∑(rxf)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058k + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.029)i + (-1.4P + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4P + 2.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
Ahora a encontrar Ez
-1.4P + 2.058 – 2.8Ez = 0
-1.4(2.93) + 2.058 – 2.8Ez = 0
-4.102 +2.058 – 2.8Ez = 0
-2.102 – 2.8Ez = 0
– 2.8Ez = 2.102
[b]Ez = - 0.75 kN['b]
CA = √((1.4) ² + (1.4) ²+(0.7)²) = 2.1
FCA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = -1.47i + 1.47j – 0.73k
FCB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = 1.47i + 1.47j – 0.73k
∑F = 0
(Dx + Ex – 1.47 + 1.47 )i + (Dy + Ey + 1.47 +1.47 )j + (Dz + Ez – 0.73 -0.73 + P )k = 0
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
Despejamos:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
∑FD = ∑(rxf)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058k + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.029)i + (-1.4P + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4P + 2.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
Ahora a encontrar Ez
-1.4P + 2.058 – 2.8Ez = 0
-1.4(2.93) + 2.058 – 2.8Ez = 0
-4.102 +2.058 – 2.8Ez = 0
-2.102 – 2.8Ez = 0
– 2.8Ez = 2.102
[b]Ez = - 0.75 kN['b]
RL081194- Invitado
MARIA SILVINA SUAREZ
SN080769 Dom 08 Jun 2008, 16:25
PERDON POR LA TARDANZA PERO ACABO DE REGRESAR
... HOY SI AHI LE VA... BUENO OJALA ESTE BN... SINO PUES HAY NOS EXPLICA COMO ERA OK! 
PROBLEMA 4
TANTO LOS SEGMENTOS CA COMO CB SON IGUALES POR LO TANTO: CA = CB
CA = √((1.4) ² + (1.4) ²+(0.7)²) = 2.1
CB = √((1.4) ² + (1.4) ²+(0.7)²) = 2.1
YA CON ESTO SE PUEDEN BUSCAR LAS FUERZAS EN CA Y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
OCUPANDO LA CONDICION DE EQUILIBRIO DE FUERZAS
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k=0
POR LO TANTO:
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
AHORA DESPEJANDO LAS INCOGNITAS EN LAS ECUACIONES ANTERIORES:
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
MOMENTOS EN “D”
∑FD = ∑(r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
POR MEDIO DE PRODUCTO VECTORIAL ENCONTRAMOS:
(-1.022i – (-2.06)k) + P(0.7i – 1.4j) + (-1.03i + 2.06k + 2.06k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.06k + 0.7i P – 1.4j P -1.03i + 2.06j + 2.06k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.03)i + (-1.4P + 2.06 – 2.8Ez)j + (2.06 + 2.06 + 2.8Ey)k=0
DE AHÍ AL AGRUPAR SE OBTIENEN LAS 3 ECUACIONES:
∑Mx = -1.022 + 0.7 P – 1.03 = 0 (1)
∑My = -1.4p + 1.06 – 2.8Ez = 0 (2)
∑Mz = 2.06 + 2.06 + 2.8Ey = 0 (3)
DESPEJANDO P en (1)
-1.022 + 0.7 P – 1.03 = 0
0.7 P = 1.022 + 1.03
P = 2.052/ 0.7
P = 2.931 kN (ESTA ES LA FUERZA MAXIMA Q PODRIA TENER EL VIENTO)
DESPEJANDO Ez EN (2)
-1.4 + 1.06 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.06
Ez = -0.34/– 2.8
Ez = 0.121 kN (ESTA ES LA REACCION EN LA COMPONENTE DE E EN Z)
SN080769- Invitado
Pamela Sermeño
SR080811 Dom 08 Jun 2008, 16:26
Primero encontramos el valor de los vectores AC y BC con sus componentes:
CA = -1.4i +1.4j -0.7k
CA = [(-1.4) ^2 + (1.4)^ 2+(-0.7)^2]^1/2
CA = [4.41]^1/2
CA = 2.1
CB = [(1.4) ^2 + (1.4)^ 2+(-0.7)^2]^1/2
CB = [4.41] ^1/2
CB = 2.1
CA = (-1.4i + 1.4j – 0.7k)/2.1 = -0.67i + 0.67j – 0.33k
CB = (1.4i + 1.4j -0.7k)/2.1 = 0.67i + 0.67j – 0.33k
Para encontrar las fuerzas en CA y en CB se multiplica x 2.2kN
CA = (2.2kN) x (-0.67i + 0.67j – 0.33k) = (-1.47i + 1.47j – 0.73)kN
CB = (2.2kN) x (0.67i + 0.67j – 0.33k) = (1.47i + 1.47j – 0.73)kN
Sumatorias de Fuerzas:
∑ F= 0
(Dx +Ex – CAx + CBx)i +(Dy + Ey + CAy +CBy)j + (Dz + Ez – CAz -CBz + P)k = 0
(Dx+Ex – 1.47 + 1.47)i +(Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
∑Fx= 0
(Dx+Ex – 1.47 + 1.47)i = 0
∑Fy= 0
(Dy + Ey + 1.47 +1.47)j = 0
∑Fz= 0
(Dz + Ez – 0.73 -0.73 + P)k = 0
Dx+Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 - P
∑M = 0
MACz + MBCz + MP = 0
(-0.73kN).(1.4m) + (-0.73kN).(1.4m) + MP.(0.7m) = 0
-1.02kN.m – 1.02kN.m + 0.7mMP = 0
-2.04 KN.m + 0.7mMp = 0
MP = 2.04kN.m / 0.7m
MP = 2.91 kN
Al sumar los momentos en D obtenemos:
∑FD = r x F
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Resolviendo por producto vectorial:
(-1.022i–(-2.058)k) +P(0.7i – 1.4j)+(-1.029i + 2.058j + 2.058k)+(2.8 )(Eyk –Ezj) =0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Ahora Tendremos:
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
∑Mx = -1.022 + 0.7 P – 1.029 = 0
∑My = -1.4p + 1.058 – 2.8Ez = 0
∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Hallando Ez:
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Pmax = 2.91kN
Ez = 0.122kN
CA = -1.4i +1.4j -0.7k
CA = [(-1.4) ^2 + (1.4)^ 2+(-0.7)^2]^1/2
CA = [4.41]^1/2
CA = 2.1
CB = [(1.4) ^2 + (1.4)^ 2+(-0.7)^2]^1/2
CB = [4.41] ^1/2
CB = 2.1
CA = (-1.4i + 1.4j – 0.7k)/2.1 = -0.67i + 0.67j – 0.33k
CB = (1.4i + 1.4j -0.7k)/2.1 = 0.67i + 0.67j – 0.33k
Para encontrar las fuerzas en CA y en CB se multiplica x 2.2kN
CA = (2.2kN) x (-0.67i + 0.67j – 0.33k) = (-1.47i + 1.47j – 0.73)kN
CB = (2.2kN) x (0.67i + 0.67j – 0.33k) = (1.47i + 1.47j – 0.73)kN
Sumatorias de Fuerzas:
∑ F= 0
(Dx +Ex – CAx + CBx)i +(Dy + Ey + CAy +CBy)j + (Dz + Ez – CAz -CBz + P)k = 0
(Dx+Ex – 1.47 + 1.47)i +(Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
∑Fx= 0
(Dx+Ex – 1.47 + 1.47)i = 0
∑Fy= 0
(Dy + Ey + 1.47 +1.47)j = 0
∑Fz= 0
(Dz + Ez – 0.73 -0.73 + P)k = 0
Dx+Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 - P
∑M = 0
MACz + MBCz + MP = 0
(-0.73kN).(1.4m) + (-0.73kN).(1.4m) + MP.(0.7m) = 0
-1.02kN.m – 1.02kN.m + 0.7mMP = 0
-2.04 KN.m + 0.7mMp = 0
MP = 2.04kN.m / 0.7m
MP = 2.91 kN
Al sumar los momentos en D obtenemos:
∑FD = r x F
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Resolviendo por producto vectorial:
(-1.022i–(-2.058)k) +P(0.7i – 1.4j)+(-1.029i + 2.058j + 2.058k)+(2.8 )(Eyk –Ezj) =0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Ahora Tendremos:
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
∑Mx = -1.022 + 0.7 P – 1.029 = 0
∑My = -1.4p + 1.058 – 2.8Ez = 0
∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Hallando Ez:
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Pmax = 2.91kN
Ez = 0.122kN
SR080811- Invitado
Luis Oviedo
OL060905 Dom 08 Jun 2008, 18:24
me va a disculpar ing. pero me costo un poco entender este problema, y aun todavia tengo dudas y
si ve similitud con otra respuesta es porque pase un buen rato hablando con un compañero porque le pedi que me explicara mas o menos porque no sabia por donde comenzar....
me gustaria que resolvieramos el ejercicio en clases....
Problema 4
Vector CA y vector CB son iguales….
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA=√4.41= 2.1
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
y se consiguen las siguientes ecuaciones…
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
se tiene que….
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
∑MD = 0
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Por pro. Vectorial….
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.2 (Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Agrupamos:
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
tenemos que..
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Buscando P
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
buscando Ez
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
si ve similitud con otra respuesta es porque pase un buen rato hablando con un compañero porque le pedi que me explicara mas o menos porque no sabia por donde comenzar....
me gustaria que resolvieramos el ejercicio en clases....
Problema 4
Vector CA y vector CB son iguales….
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA=√4.41= 2.1
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
∑F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
y se consiguen las siguientes ecuaciones…
∑Fx = Dx + Ex – 1.47 + 1.47 = 0
∑Fy = Dy + Ey + 1.47 +1.47 = 0
∑Fz = Dz + Ez – 0.73 -0.73 + P= 0
se tiene que….
Dx + Ex = 0
Dy + Ey = -2.94
Dz + Ez = 1.46 – P
∑MD = 0
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Por pro. Vectorial….
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.2 (Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
Agrupamos:
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
tenemos que..
Ec. 1: ∑Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: ∑My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: ∑Mz = 2.058 + 2.058 + 2.8Ey = 0
Buscando P
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
buscando Ez
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
OL060905- Invitado
Giovanni Calles
CP080899 Dom 08 Jun 2008, 19:03
Los vectores CA = CB
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA = √4.41= 2.1
CA = 2.1
CB = 2.1
Buscado los vectores unitarios CA y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
La Sumatorias de fuerza
F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
Entonces se tiene:
Fx =
Dx + Ex – 1.47 + 1.47 = 0
Dx + Ex = 0
Fy =
Dy + Ey + 1.47 +1.47 = 0
Dy + Ey = -2.94
Fz = Dz + Ez – 0.73 -0.73 + P= 0
Dz + Ez = 1.46 – P
Sumatoria de momentos en D
FD = (r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Producto vectorial:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Entonces tiene 3 ecuaciones:
Ec. 1: Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: Mz = 2.058 + 2.058 + 2.8Ey = 0
Encontrando P en Ecuacion 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
Encontrando Ez en Ecuacion 2
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Encontrando Ey de ecuacion 3
2.058 + 2.058 + 2.8Ey = 0
2.8Ey = -2.058-2.058
2.8Ey = -4.66
Ey = 1.66 kN
CA = ((1.4) ² + (1.4) ²+(0.7)²) = 4.41
CA = √4.41= 2.1
CA = 2.1
CB = 2.1
Buscado los vectores unitarios CA y CB
CA = (2.2)(-1.4i + 1.4j – 0.7k)/2.1 = (-1.47i + 1.47j – 0.73k)
CB = (2.2)(1.4i + 1.4j -0.7k)/2.1 = (1.47i + 1.47j – 0.73k)
La Sumatorias de fuerza
F = 0
(Dx + Ex – 1.47 + 1.47)i + (Dy + Ey + 1.47 +1.47)j + (Dz + Ez – 0.73 -0.73 + P)k = 0
Entonces se tiene:
Fx =
Dx + Ex – 1.47 + 1.47 = 0
Dx + Ex = 0
Fy =
Dy + Ey + 1.47 +1.47 = 0
Dy + Ey = -2.94
Fz = Dz + Ez – 0.73 -0.73 + P= 0
Dz + Ez = 1.46 – P
Sumatoria de momentos en D
FD = (r x f)
(1.4j)X(-1.47i + 1.47j – 0.73k ) + (1.4i + 0.7j)X(Pk) + (1.4i + 0.7k)X(1.47i + 1.47j – 0.73k) + (2.8i)X(Exi + Eyj + Ezk) = 0
Producto vectorial:
(-1.022i – (-2.058)k) + P(0.7i – 1.4j) + (-1.029i + 2.058j + 2.058k) + (2.(Eyk –Ezj) = 0
-1.022i + 2.058k + 0.7i P – 1.4j P -1.029i + 2.058j + 2.058k + 2.8Eyk –2.8Ezj= 0
(-1.022 + 0.7 P – 1.029)i + (-1.4p + 2.058 – 2.8Ez)j + (2.058 + 2.058 + 2.8Ey)k = 0
Entonces tiene 3 ecuaciones:
Ec. 1: Mx = -1.022 + 0.7 P – 1.029 = 0
Ec. 2: My = -1.4p + 1.058 – 2.8Ez = 0
Ec. 3: Mz = 2.058 + 2.058 + 2.8Ey = 0
Encontrando P en Ecuacion 1
-1.022 + 0.7 P – 1.029 = 0
0.7 P = 1.022 + 1.029
0.7 P = 2.051
P = 2.93 kN
Encontrando Ez en Ecuacion 2
-1.4 + 1.058 – 2.8Ez = 0
– 2.8Ez = 1.4 - 1.058
– 2.8Ez = -0.342
Ez = 0.122 kN
Encontrando Ey de ecuacion 3
2.058 + 2.058 + 2.8Ey = 0
2.8Ey = -2.058-2.058
2.8Ey = -4.66
Ey = 1.66 kN
CP080899- Invitado
Página 1 de 2. • 1, 2
TECNICO MANTENIMIENTO AERONAUTICO :: Auxiliar :: MOMENTOS Y REACCIONES EN VIGAS Y ESTRUCTURAS_080608
Página 1 de 2.
Permisos de este foro:
No puedes responder a temas en este foro.