PROBLEMA No. 2
TECNICO MANTENIMIENTO AERONAUTICO :: Auxiliar :: MOMENTOS Y REACCIONES EN VIGAS Y ESTRUCTURAS_080608
Página 3 de 3.
Página 3 de 3. •  1, 2, 3
1, 2, 3
 Ejercicio2
Ejercicio2
RONALD BENJAMIN RAMOS PUTUN
ƩFx=0
-Rax + 1000/tang 10 + Rb = 0
ƩFy=0
Fay - 1000=0
ƩFMa=0
1000(12) + Rb(3.47) = 0
Rb(3.47) =-12000
Rb= -12000/3.47lb
Rb= 3458.21
-Rax + 1000/tang10 + (-3458.21)=0
Rax= 2213.07 lb
ƩFx=0
-Rax + 1000/tang 10 + Rb = 0
ƩFy=0
Fay - 1000=0
ƩFMa=0
1000(12) + Rb(3.47) = 0
Rb(3.47) =-12000
Rb= -12000/3.47lb
Rb= 3458.21
-Rax + 1000/tang10 + (-3458.21)=0
Rax= 2213.07 lb
RRP06049- Invitado
 CORRECCION DE TITULO DE PROBLEMA TRUJILLO
CORRECCION DE TITULO DE PROBLEMA TRUJILLO
PERDON EL ANTERIOR ES EL NUMERO 2... SOLO ESO CORRIJO ES MI RESPUESTA PARA EL NUMERO 2 
TM080812- Invitado
 Jose Mata
Jose Mata
bueno aki esta mi rspuesta todo esta en imagnes espero q lo pueda ver y no tenga ningun inconveniente para abrir la imagen, el ejercicio esta dividido en 3 imagenes:
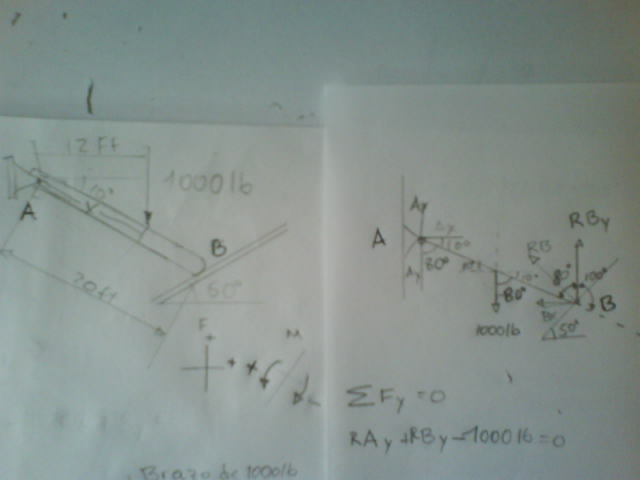
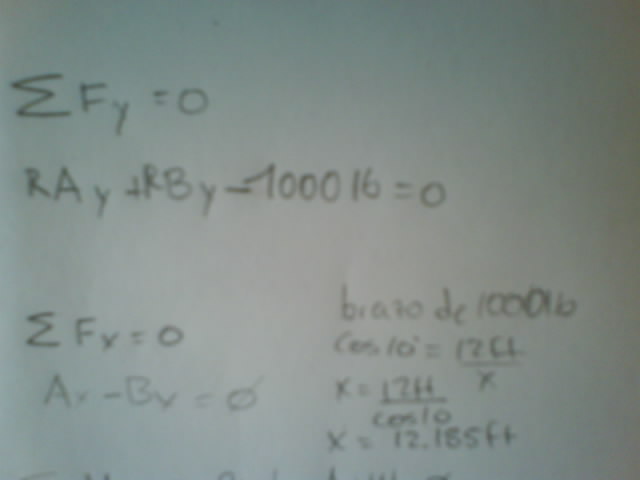


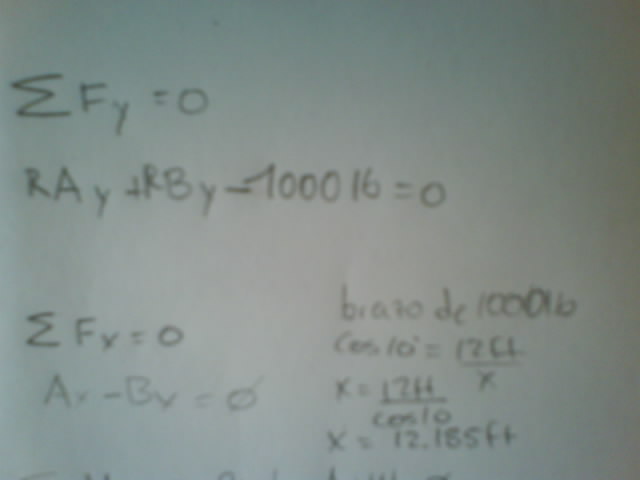

mm080805- Invitado
 MARIO TRUJILLO SEGURIDAD
MARIO TRUJILLO SEGURIDAD
POR SI HAY CONFUSIÓN ESTE ES LA RESOLUCIÓN AL PROBLEMA 2
BUENO PRIMERO TENDREMOS QUE:
EFx = 0
Ax - Bsin50° = 0
EFy = 0
Ay + Bcos50° -1000 = 0
DESPUES LOS MOMENTOS DE TORSIÓN RESPECTIVOS
Sumatoria MA = 0
(20 cos10°)(Bcos50°) - (20sin10°)(Bsin50°) - 12(1000) = 0
12.66B - 2.66B - 12000 = 0
10B = 12000
B = 1200
Hallaremos Ax y Ay:
Ax - Bsin50° = 0
Ax = 1200(sin50°)
Ax = 919.2
Ay + Bcos50° - 1000 = 0
Ay = 1000 - 771.35
Ay = 228.6
PARA encontrar la reaccion en A teniendo las components de la reacción , por Pitágoras encontraremos la resultante que es la que buscamos
A= Raíz de (919.2 al cuadrado) + (228.6 al cuadrado)
A= 947.19
BUENO PRIMERO TENDREMOS QUE:
EFx = 0
Ax - Bsin50° = 0
EFy = 0
Ay + Bcos50° -1000 = 0
DESPUES LOS MOMENTOS DE TORSIÓN RESPECTIVOS
Sumatoria MA = 0
(20 cos10°)(Bcos50°) - (20sin10°)(Bsin50°) - 12(1000) = 0
12.66B - 2.66B - 12000 = 0
10B = 12000
B = 1200
Hallaremos Ax y Ay:
Ax - Bsin50° = 0
Ax = 1200(sin50°)
Ax = 919.2
Ay + Bcos50° - 1000 = 0
Ay = 1000 - 771.35
Ay = 228.6
PARA encontrar la reaccion en A teniendo las components de la reacción , por Pitágoras encontraremos la resultante que es la que buscamos
A= Raíz de (919.2 al cuadrado) + (228.6 al cuadrado)
A= 947.19
TM080812- Invitado
 Oscar Rosales - Respuesta Problema 2
Oscar Rosales - Respuesta Problema 2
Ecuación 1:
ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
Ecuación 2:
ƩFy=0
-F + FA + FB sen 220º =0x
-1000 + FA + (-0.64FB) = 0
Sumatoria de Torques:
ƩT= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Analizando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb

ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
Ecuación 2:
ƩFy=0
-F + FA + FB sen 220º =0x
-1000 + FA + (-0.64FB) = 0
Sumatoria de Torques:
ƩT= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Analizando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb

RC080896- Invitado
 Problema 2
Problema 2
Alvaro Roberto Ambrogi Escobar
para comenzar, he tomado como referencia lo siguiente:
- La reaccion en el punto A la llame R1y.
- La reaccion en el punto B la llame R2y.
- Para las fuerzas que se dirigen hacia arriba, el signo correspondiente es positivo (+).
- Para las fuerzas que se dirigen hacia abajo, el signo correspondiente es negativo (-).
- Para los momentos en sentido horario, el signo correspondiente es positivo (+).
- Para los momentos en sentido anti-horario, el signo correspondiente es negativo (-).
∑ F = 0
∑ Fx = 0
∑ Fy = 0
R1 - 1000 lbf + R2
R1y sen10º + R2y sen50º = 1000 lbf (ecuacion 1)
Como tenemos dos incognitas, procedemos realizar sumatoria de momentos para encontrar una de las reacciones y asi poder dar solucion al ejercicio.
∑ M = 0
1000 lbf (12ft) - R2 (20ft) = 0
1000 lbf (12ft) - R2y sen50º (20ft) = 0
R2y sen50º (20ft) = 1000 lbf (12ft)
R2y = 1000 lbf (12ft) / sen50º (20ft)
R2y = 12000 lbf - ft / 15.32 ft (y con esto eliminamos los ft para obtener unicamente lbf)
R2y = 783.29 lbf
ahora que tenemos el valor de R2y, procedemos a sustituir en la ecuacion 1 y encontrar el valor de R1y asi:
R1y sen10º + R2y sen50º = 1000 lbf
R1y sen10º = 1000 lbf - 783.29 lbf (sen50º)
R1y = 1000 lbf - 600.03 lbf / sen10º
R1y = 399.97 lbf/ sen10º
R1y = 2303.33 lbf


para comenzar, he tomado como referencia lo siguiente:
- La reaccion en el punto A la llame R1y.
- La reaccion en el punto B la llame R2y.
- Para las fuerzas que se dirigen hacia arriba, el signo correspondiente es positivo (+).
- Para las fuerzas que se dirigen hacia abajo, el signo correspondiente es negativo (-).
- Para los momentos en sentido horario, el signo correspondiente es positivo (+).
- Para los momentos en sentido anti-horario, el signo correspondiente es negativo (-).
∑ F = 0
∑ Fx = 0
∑ Fy = 0
R1 - 1000 lbf + R2
R1y sen10º + R2y sen50º = 1000 lbf (ecuacion 1)
Como tenemos dos incognitas, procedemos realizar sumatoria de momentos para encontrar una de las reacciones y asi poder dar solucion al ejercicio.
∑ M = 0
1000 lbf (12ft) - R2 (20ft) = 0
1000 lbf (12ft) - R2y sen50º (20ft) = 0
R2y sen50º (20ft) = 1000 lbf (12ft)
R2y = 1000 lbf (12ft) / sen50º (20ft)
R2y = 12000 lbf - ft / 15.32 ft (y con esto eliminamos los ft para obtener unicamente lbf)
R2y = 783.29 lbf
ahora que tenemos el valor de R2y, procedemos a sustituir en la ecuacion 1 y encontrar el valor de R1y asi:
R1y sen10º + R2y sen50º = 1000 lbf
R1y sen10º = 1000 lbf - 783.29 lbf (sen50º)
R1y = 1000 lbf - 600.03 lbf / sen10º
R1y = 399.97 lbf/ sen10º
R1y = 2303.33 lbf

AE060644- Invitado
 Rafael Murillo GT01
Rafael Murillo GT01
Resolución de Ejercicio 2:
ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
ƩFy=0
-F + FA + FB sen 220º =0x
-1000 + FA + (-0.64FB) = 0
Sumatoria de Torques:
ƩT= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Analizando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb
ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
ƩFy=0
-F + FA + FB sen 220º =0x
-1000 + FA + (-0.64FB) = 0
Sumatoria de Torques:
ƩT= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Analizando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb
MA080802- Invitado
 Rafael Gil GT01
Rafael Gil GT01
Rafael Gil
Desarrollo de ejercicio 2:
Sumatoria de fuerzas en eje x:
ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
Sumatoria de fuerzas en eje y:
ƩFy=0
-F + FA + FB sen 220º =0x
-1000 + FA + (-0.64FB) = 0
Sumatoria de momentos:
ƩM= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Analizando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb
Desarrollo de ejercicio 2:
Sumatoria de fuerzas en eje x:
ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
Sumatoria de fuerzas en eje y:
ƩFy=0
-F + FA + FB sen 220º =0x
-1000 + FA + (-0.64FB) = 0
Sumatoria de momentos:
ƩM= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Analizando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb
GB080941- Invitado
 Francisco Caminos
Francisco Caminos
Francisco Caminos CR080944
ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
(ecuacion 1)
ƩFy=0
-F + FA + FB sen 220º =0
-1000 + FA + (-0.64FB) = 0
(ecuacion 2)
ƩMa= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Encontrando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb

ƩFx=0
FA+FB cos 220º = 0
FA + (-0.76 FB) = 0
(ecuacion 1)
ƩFy=0
-F + FA + FB sen 220º =0
-1000 + FA + (-0.64FB) = 0
(ecuacion 2)
ƩMa= 0
-(1000)*(12) + (FB sen220º)*(19.69) + (FB cos220º)*(3.47) =0
-12000 + (-12.656 FB) + (-2.658FB) = 0
(12.656 + 2.658) FB +12000=0
15.314 FB = -12000
FB = -12000/15.314
FB = -783.596 lb
Encontrando FA:
-1000 +FA + (-0.64)FB = 0
-1000 + FA + (-0.64 * -783.569)=0
-1000 + FA + 501.484=0
FA= 1000-501.484
FA = 498.516 lb
CR080944- Invitado
 Problema No 3
Problema No 3
Alicia Maicelle Marroquín Girón
Mas o menos creo que asi va....:
Primero obtenemos:
ΣFx=0
ΣFx= RAx-RBx
ΣFy=0
ΣFy= Ay+By-1000lbsen10°
ΣM=0
ΣM= 1000lb (12ft cos 10°) -RBy sen 50 (20ft)
Ahora despejamos en cada una de las ec.
RAx-RBx + 1000 cos 10° =0
RAx = RBx - 173.65lb
Ay+By-1000lb = 0
Ay+By = 1000lbsen10°
Ay+By=984.81lb
1000lb (12ft /cos 10°) = RBy sen 50 (20ft)
1000lb(12.19ft)=RBy(0.77)(20ft)
12190lb.ft=RBy15.4ft
12190lb.ft/15.4ft = RBy
RBy = 791.56lb
RAy=1000lbsen10°-RBy
RAy=1000lbsen10°- 791.56lb
RAy= 208.44lb
RAx = RBx - 173.65lb
By=Bsen50°
B=By/sen50°
B=791.56lb/sen50°
B=1033.31lb
Bx=Bcos50°
Bx=1033.31lbcos50°
Bx=664.19lb
RAx = RBx - 173.65lb
RAx = 664.19lb - 173.65lb
RAx= 490.54lb

MG080846- Invitado
 Gerardo Benitez
Gerardo Benitez
∑Fx = 0
∑Fy = 0 Condiciones generales.
∑M = 0
Encontrando las componentes tanto en X como en Y
Componentes en Y:
FY = 1000lbcos10º
FY = 984.807
Componente en X:
FX = 1000lbsen10º
FX = 173.648
∑Fy = 0
-984.807lb + Ray = 0
Entonces:
Ray = 984.807lb
∑Fx = 0
Ray + Rby + 173.648 = 0
∑Mx = 0
∑Mx= -1000lb(12ft) + Rbx(20ft)= 0
Despejando Rbx:
Rbx = 1000lb(12ft)/20ft
Rbx = 600lb
∑My= 0
Rby = 0(Esto debido a la falta de friccion por lo tanto el momento es 0)
Despejando Rax de la ecuación:
Ray + Rax + 173.648lb= 0
Entonces:
Rax = 173.648lb + Ray(600lb)
Rax = 773.648lb
∑Fy = 0 Condiciones generales.
∑M = 0
Encontrando las componentes tanto en X como en Y
Componentes en Y:
FY = 1000lbcos10º
FY = 984.807
Componente en X:
FX = 1000lbsen10º
FX = 173.648
∑Fy = 0
-984.807lb + Ray = 0
Entonces:
Ray = 984.807lb
∑Fx = 0
Ray + Rby + 173.648 = 0
∑Mx = 0
∑Mx= -1000lb(12ft) + Rbx(20ft)= 0
Despejando Rbx:
Rbx = 1000lb(12ft)/20ft
Rbx = 600lb
∑My= 0
Rby = 0(Esto debido a la falta de friccion por lo tanto el momento es 0)
Despejando Rax de la ecuación:
Ray + Rax + 173.648lb= 0
Entonces:
Rax = 173.648lb + Ray(600lb)
Rax = 773.648lb
BD060935- Invitado
 Ruben Arana
Ruben Arana
Componentes en X y en y del peso:
Wy = 1000 Cos 10º = 984.81
Wx = 1000 Sen 10º = 173.65
Con respecto a A Momento de Torsión:
La distancia 12.19 es la distancia que hay entre el punto A y la componente en y del peso, se obtuvo con la función coseno tomando el ángulo de 10º.
∑MA = 0
Wy.d – RBy.d
(984.81lb) (12.19ft) – RBy (20ft) = 0
12004.83lb.ft = RBy (20ft)
RBy = 12004.83lb.ft / 20ft
RBy = 600.24lb
Según las componentes de la Reacción en B:
RBy = RB sen 30º
RB = 600.24lb / sen 30º
RB = 1200.48lb
∑Fx = 0
Ax + Wx – RBcos30º = 0
Ax = RBcos30º - Wx
Ax = (1200.48. cos30º) – 173.65lb
Ax = 1039.65lb -173.65lb
Ax = 866lb
∑Fy= 0
Ay – Wy + RBsen30º = 0
Ay – 984.81lb + 600.24lb = 0
Ay -384.57lb = 0
Ay = 384.57lb
A = √ (866)^2 + (384.57)^2
A = √ 897850.08
A = 947.55lb
RA = 947.55lb
RB = 1200.48lb
Wy = 1000 Cos 10º = 984.81
Wx = 1000 Sen 10º = 173.65
Con respecto a A Momento de Torsión:
La distancia 12.19 es la distancia que hay entre el punto A y la componente en y del peso, se obtuvo con la función coseno tomando el ángulo de 10º.
∑MA = 0
Wy.d – RBy.d
(984.81lb) (12.19ft) – RBy (20ft) = 0
12004.83lb.ft = RBy (20ft)
RBy = 12004.83lb.ft / 20ft
RBy = 600.24lb
Según las componentes de la Reacción en B:
RBy = RB sen 30º
RB = 600.24lb / sen 30º
RB = 1200.48lb
∑Fx = 0
Ax + Wx – RBcos30º = 0
Ax = RBcos30º - Wx
Ax = (1200.48. cos30º) – 173.65lb
Ax = 1039.65lb -173.65lb
Ax = 866lb
∑Fy= 0
Ay – Wy + RBsen30º = 0
Ay – 984.81lb + 600.24lb = 0
Ay -384.57lb = 0
Ay = 384.57lb
A = √ (866)^2 + (384.57)^2
A = √ 897850.08
A = 947.55lb
RA = 947.55lb
RB = 1200.48lb
AC080786- Invitado
 problema 2
problema 2
Luciano Alberto Calderòn Crespìn
- El punto A es R1. y el punto B es R2.
- Fuerzas dirigidas hacia arriba son positivas +, y hacia abajo negativcas -.
- Par en sentido horario positivo+, y Par en sentido anti horario negativo -.
∑ F = 0
∑ Fx = 0
∑ Fy = 0
R1 - 1000 lbf + R2
R1 sen10º + R2 sen50º = 1000 lbf
Hasta el momento obtenemos la ecuación anterior con dos incógnitas entonces hacemos sumatoria de momentos.
∑ M = 0
1000 lbf (12ft) - R2 (20ft) = 0
1000 lbf (12ft) - R2y sen50º (20ft) = 0
R2 sen50º (20ft) = 1000 lbf (12ft)
R2 = 1000 lbf (12ft)
sen50º (20ft)
R2 = 12000 lbf
15.32 ft
R2 = 783.29 lbf
Tenemos R2 y lo sustituimos:
R1 sen10º + R2 sen50º = 1000 lbf
R1 sen10º = 1000 lbf - 783.29 lbf (sen50º)
R1 = 1000 lbf - 600.03 lbf
sen10º
R1 = 399.97 lbf
sen10º
R1 = 2303.33 lbf
- El punto A es R1. y el punto B es R2.
- Fuerzas dirigidas hacia arriba son positivas +, y hacia abajo negativcas -.
- Par en sentido horario positivo+, y Par en sentido anti horario negativo -.
∑ F = 0
∑ Fx = 0
∑ Fy = 0
R1 - 1000 lbf + R2
R1 sen10º + R2 sen50º = 1000 lbf
Hasta el momento obtenemos la ecuación anterior con dos incógnitas entonces hacemos sumatoria de momentos.
∑ M = 0
1000 lbf (12ft) - R2 (20ft) = 0
1000 lbf (12ft) - R2y sen50º (20ft) = 0
R2 sen50º (20ft) = 1000 lbf (12ft)
R2 = 1000 lbf (12ft)
sen50º (20ft)
R2 = 12000 lbf
15.32 ft
R2 = 783.29 lbf
Tenemos R2 y lo sustituimos:
R1 sen10º + R2 sen50º = 1000 lbf
R1 sen10º = 1000 lbf - 783.29 lbf (sen50º)
R1 = 1000 lbf - 600.03 lbf
sen10º
R1 = 399.97 lbf
sen10º
R1 = 2303.33 lbf
cc060669- Invitado
 Pamela Sermeño
Pamela Sermeño
Para el peso
Wy = 1000 Cos 10º = 984.81
Wx = 1000 Sen 10º = 173.65
Los momentos de torsión para el punto A
Para la distancia del punto A, a la componente vertical del peso se encuentra asi:
d = 12ft / cos10º = 12.19ft
∑MA = 0
Wy.d – RBy.d
(984.81lb) (12.19ft) – RBy (20ft) = 0
12004.83lb.ft = RBy (20ft)
RBy = 12004.83lb.ft / 20ft
RBy = 600.24lb
Según las componentes de la Reacción en B:
RBy = RB sen 30º
RB = 600.24lb / sen 30º
RB = 1200.48lb
∑Fx = 0
Ax + Wx – RBcos30º = 0
Ax = RBcos30º - Wx
Ax = (1200.48. cos30º) – 173.65lb
Ax = 1039.65lb -173.65lb
Ax = 866lb
∑Fy= 0
Ay – Wy + RBsen30º = 0
Ay – 984.81lb + 600.24lb = 0
Ay -384.57lb = 0
Ay = 384.57lb
A = [(866)^2 + (384.57)^2]^1/2
A = [897850.08]^1/2
A = 947.55lb
RA = 947.55lb
RB = 1200.48lb
Wy = 1000 Cos 10º = 984.81
Wx = 1000 Sen 10º = 173.65
Los momentos de torsión para el punto A
Para la distancia del punto A, a la componente vertical del peso se encuentra asi:
d = 12ft / cos10º = 12.19ft
∑MA = 0
Wy.d – RBy.d
(984.81lb) (12.19ft) – RBy (20ft) = 0
12004.83lb.ft = RBy (20ft)
RBy = 12004.83lb.ft / 20ft
RBy = 600.24lb
Según las componentes de la Reacción en B:
RBy = RB sen 30º
RB = 600.24lb / sen 30º
RB = 1200.48lb
∑Fx = 0
Ax + Wx – RBcos30º = 0
Ax = RBcos30º - Wx
Ax = (1200.48. cos30º) – 173.65lb
Ax = 1039.65lb -173.65lb
Ax = 866lb
∑Fy= 0
Ay – Wy + RBsen30º = 0
Ay – 984.81lb + 600.24lb = 0
Ay -384.57lb = 0
Ay = 384.57lb
A = [(866)^2 + (384.57)^2]^1/2
A = [897850.08]^1/2
A = 947.55lb
RA = 947.55lb
RB = 1200.48lb
SR080811- Invitado
 Oswaldo Antonio Berrios Chavarria
Oswaldo Antonio Berrios Chavarria
Respuesta Problema 2
Primero sacamos longitudes:
Longitud barra: 20ft
L1: 20ft (cos 10º) = 19.76ft
L2: 12ft [esta ya la conocemos por el dibujo]
L3: 20ft (sen 10º) = 3.47ft
Sacando componentes de fuerza de "B"
FBx = B (cos 50º)
FBy = B (sen 50º)
Sacando la sumatoria de momentos:
∑M = 0
∑M = (L1)(FBx) - (L3)(FBy) - (L2)(1000lb)
∑M = (19.67 ft)((B)(Cos 50º)) – (3.47 ft)((B)(Sen 50º)) – (12 ft)(1000lb)
∑M = (B)(19.67 ft)(Cos 50º) – (B)(3.47 ft)(Sen 50º) – (12 ft)(1000lb)
∑M = (B)(12.64 ft)– (B)(2.66 ft) – (12000ft.lb)
∑M = (B)(9.98 ft) – (12000ft.lb)
(B)(9.98 ft) – (12000ft.lb) = 0
(B)(9.98 ft) = 12000ft.lb
B = 12000ft.lb / 9.98ft
B = 1202.40 lb
∑Fx = 0
∑Fx = FAx – FBx = 0
FAx – (B)(Sen 50º) = 0
FAx = (B)(Sen 50º)
FAx = (1202.40 lb)(Sen 50º) = 921.09 lb
RAx = 921.09 lb
∑Fy = 0
∑Fy = FAy + FBy – 1000 lb = 0
FAy + FBy – 1000 lb = 0
FAy = -FBy + 1000 lb
FAy = (-B)(Cos 50º) + 1000 lb
FAy = -772.9 + 1000 lb
FAy = 227.11 lb
RAy = 227.11 lb
Primero sacamos longitudes:
Longitud barra: 20ft
L1: 20ft (cos 10º) = 19.76ft
L2: 12ft [esta ya la conocemos por el dibujo]
L3: 20ft (sen 10º) = 3.47ft
Sacando componentes de fuerza de "B"
FBx = B (cos 50º)
FBy = B (sen 50º)
Sacando la sumatoria de momentos:
∑M = 0
∑M = (L1)(FBx) - (L3)(FBy) - (L2)(1000lb)
∑M = (19.67 ft)((B)(Cos 50º)) – (3.47 ft)((B)(Sen 50º)) – (12 ft)(1000lb)
∑M = (B)(19.67 ft)(Cos 50º) – (B)(3.47 ft)(Sen 50º) – (12 ft)(1000lb)
∑M = (B)(12.64 ft)– (B)(2.66 ft) – (12000ft.lb)
∑M = (B)(9.98 ft) – (12000ft.lb)
(B)(9.98 ft) – (12000ft.lb) = 0
(B)(9.98 ft) = 12000ft.lb
B = 12000ft.lb / 9.98ft
B = 1202.40 lb
∑Fx = 0
∑Fx = FAx – FBx = 0
FAx – (B)(Sen 50º) = 0
FAx = (B)(Sen 50º)
FAx = (1202.40 lb)(Sen 50º) = 921.09 lb
RAx = 921.09 lb
∑Fy = 0
∑Fy = FAy + FBy – 1000 lb = 0
FAy + FBy – 1000 lb = 0
FAy = -FBy + 1000 lb
FAy = (-B)(Cos 50º) + 1000 lb
FAy = -772.9 + 1000 lb
FAy = 227.11 lb
RAy = 227.11 lb
BC060610- Invitado
 OCTAVIO AMAYA
OCTAVIO AMAYA
DANIEL OCTAVIO AMAYA ARAUZ AA070857
RESOLUCION PROBLEMA #2
A+B-1000=0
A+B=1000 lb
-A(20cos10)+ 1000 lb (8ft)= 0
A=(-8000 lb/ft)/(-20cos10 ft)
A=406.17 lb
B=1000 lb-406.17 lb
B=593.89 lb
NO TIENE COMPONENTES EN X PORQUE APESAR QUE LAS FUERZAS ESTAN PROYECTADAS SOBRE LA HORIZONTAL; ESTAS ESTAN EJERCIENDOSE SOBRE LA VERTICAL.
RESOLUCION PROBLEMA #2
A+B-1000=0
A+B=1000 lb
-A(20cos10)+ 1000 lb (8ft)= 0
A=(-8000 lb/ft)/(-20cos10 ft)
A=406.17 lb
B=1000 lb-406.17 lb
B=593.89 lb
NO TIENE COMPONENTES EN X PORQUE APESAR QUE LAS FUERZAS ESTAN PROYECTADAS SOBRE LA HORIZONTAL; ESTAS ESTAN EJERCIENDOSE SOBRE LA VERTICAL.
AA070857- Invitado
 CARLOS AMAYA
CARLOS AMAYA
RESPUESTA AL EJERCICIO #3
A+B-1000=0
A+B=1000 lb
-A(20cos10)+ 1000 lb (8ft)= 0
A=(-8000 lb/ft)/(-20cos10 ft)
A=406.17 lb
B=1000 lb-406.17 lb
B=593.89 lb
A+B-1000=0
A+B=1000 lb
-A(20cos10)+ 1000 lb (8ft)= 0
A=(-8000 lb/ft)/(-20cos10 ft)
A=406.17 lb
B=1000 lb-406.17 lb
B=593.89 lb
aa080754- Invitado
Página 3 de 3. •  1, 2, 3
1, 2, 3
TECNICO MANTENIMIENTO AERONAUTICO :: Auxiliar :: MOMENTOS Y REACCIONES EN VIGAS Y ESTRUCTURAS_080608
Página 3 de 3.
Permisos de este foro:
No puedes responder a temas en este foro.