PREGUNTA 01

Una pregunta ing....

¿El xx y yy son los ejes centroidales..???

Ramos putun ronald benjamin

Buenos dias ing...

Tengo la duda para sacar los momentos de inercia hay que tomar los ejes centroidales o los ejes normales de X y Y..

AREA X Y DX DY
1 20cm2 1cm 15cm 4.67cm 5.33cm
2 20cm2 7cm 11cm 0.67cm 0.67cm
3 20cm2 11cm 5cm 5.33cm 4.67cm


Area 1 = B x H
Area 1 = (2cm)(10cm)
Area 1= 20cm2

Area 2= B x H
Area 2= (10cm)(2cm)
Area 2= 20cm2

Area 3 = B x H
Area 3 = (2cm)(10cm)
Area 3= 20 cm2

Xc= (20cm2)(1cm)+ (20cm2)(7cm) + (20cm2)(11) / 60 cm2
Xc = 380 cm3 /60 cm2
Xc= 6.33 cm

Yc = (20cm2)(15cm) + (20cm2)(11cm) + (20cm2)(5cm) / 60cm2
Yc =620 cm3 / 60cm2
Yc =10.33 cm


Iox1 = B x H3 / 12 + (20cm2)(4.67cm)2
Iox1 = (2cm) x (10cm)3 /12 + 436.2 cm4
Iox1 = 166.7 cm4 + 436.2 cm4
Iox1 = 602.9 cm4

Iox2 = B x H3 /12 + (20cm2)(0.67cm)2
Iox2 = (10cm) x (2cm)3 /12 + 8.978 cm4
Iox2 = 6.667 cm4 + 8.978 cm4
Iox2 = 15.65 cm4

Iox3 = B x H3 /12 + (20cm2)(5.33cm)2
Iox3 = (2cm) x (10cm)3 / 12 + 568.2 cm4
Iox3 = 166.7cm4 + 568.2 cm4
Iox3 = 734.9 cm4

Ioxtotal: Iox1 + Iox2 + Iox3
Ioxtotal: 602.9cm4 + 15.65 cm4 + 734.9 cm4
Ioxtotal: 1353 cm4

Ioy1 = B3 x H /12 + (20cm2)(5.33cm)2
Ioy1 = (2cm)3 x (10cm) /12 + 568.2 cm4
Ioy1 = 6.667 cm4 + 568.2 cm4

Ioy2 = B3 x H /12 + (20cm2)(0.67cm)2
Ioy2 = (10cm)3 x (2cm) /12 + 8.978 cm4
Ioy2 = 166.7 cm4 + 8.978 cm4
Ioy2 = 175.7 cm4

Ioy3= B3 x H /12 + (20cm2)(4.67cm2)
Ioy3 = (2cm)3 x (10cm) /12 + 436.2 cm4
Ioy3 = 6.667 cm4 + 436.2 cm4
Ioy3 = 442.8 cm4

Ioytotal = Ioy1 + Ioy2 + Ioy3
Ioytotal = 574.8 cm4 + 175.7 cm4 + 442.8 cm4
Ioytotal = 1193 cm4


[b][i][u]
Eje en x = 6.33cm
Eje en y = 10.33cm

RONALD BENJAMIN RAMOS PUTUN

AREA X Y DX DY
1 20cm2 1cm 15cm 4.67cm 5.33cm
2 20cm2 7cm 11cm 0.67cm 0.67cm
3 20cm2 11cm 5cm 5.33cm 4.67cm


Area 1 = B x H
Area 1 = (2cm)(10cm)
Area 1= 20cm2

Area 2= B x H
Area 2= (10cm)(2cm)
Area 2= 20cm2

Area 3 = B x H
Area 3 = (2cm)(10cm)
Area 3= 20 cm2

Xc= (20cm2)(1cm)+ (20cm2)(7cm) + (20cm2)(11) / 60 cm2
Xc = 380 cm3 /60 cm2
Xc= 6.33 cm

Yc = (20cm2)(15cm) + (20cm2)(11cm) + (20cm2)(5cm) / 60cm2
Yc =620 cm3 / 60cm2
Yc =10.33 cm


Iox1 = B x H3 / 12 + (20cm2)(4.67cm)2
Iox1 = (2cm) x (10cm)3 /12 + 436.2 cm4
Iox1 = 166.7 cm4 + 436.2 cm4
Iox1 = 602.9 cm4

Iox2 = B x H3 /12 + (20cm2)(0.67cm)2
Iox2 = (10cm) x (2cm)3 /12 + 8.978 cm4
Iox2 = 6.667 cm4 + 8.978 cm4
Iox2 = 15.65 cm4

Iox3 = B x H3 /12 + (20cm2)(5.33cm)2
Iox3 = (2cm) x (10cm)3 / 12 + 568.2 cm4
Iox3 = 166.7cm4 + 568.2 cm4
Iox3 = 734.9 cm4

Ioxtotal: Iox1 + Iox2 + Iox3
Ioxtotal: 602.9cm4 + 15.65 cm4 + 734.9 cm4
Ioxtotal: 1353 cm4

Ioy1 = B3 x H /12 + (20cm2)(5.33cm)2
Ioy1 = (2cm)3 x (10cm) /12 + 568.2 cm4
Ioy1 = 6.667 cm4 + 568.2 cm4

Ioy2 = B3 x H /12 + (20cm2)(0.67cm)2
Ioy2 = (10cm)3 x (2cm) /12 + 8.978 cm4
Ioy2 = 166.7 cm4 + 8.978 cm4
Ioy2 = 175.7 cm4

Ioy3= B3 x H /12 + (20cm2)(4.67cm2)
Ioy3 = (2cm)3 x (10cm) /12 + 436.2 cm4
Ioy3 = 6.667 cm4 + 436.2 cm4
Ioy3 = 442.8 cm4

Ioytotal = Ioy1 + Ioy2 + Ioy3
Ioytotal = 574.8 cm4 + 175.7 cm4 + 442.8 cm4
Ioytotal = 1193 cm4


[b][i][u]
Eje en x = 6.33cm
Eje en y = 10.33cm

Determinar los momentos de inercia siguientes:
a) Ixx
b) Iyy

A A cm2 X Y
I 20 1 15
II 20 7 11
III 20 11 5

Xc= (20cm2)(1cm)+ (20cm2)(7cm) + (20cm2)(11) / 60 cm2
Xc = 380 cm3 /60 cm2
Xc= 6.33 cm

Yc = (20cm2)(15cm) + (20cm2)(11cm) + (20cm2)(5cm) / 60cm2
Yc =620 cm3 / 60cm2
Yc =10.33 cm

Con respecto a X

Iox1 = B x H3 / 12 + (20cm2)(4.67cm)2
Iox1 = (2cm) x (10cm)3 /12 + 436.2 cm4
Iox1 = 166.7 cm4 + 436.2 cm4
Iox1 = 602.84 cm4

Iox2 = B x H3 /12 + (20cm2)(0.67cm)2
Iox2 = (10cm) x (2cm)3 /12 + 8.978 cm4
Iox2 = 6.667 cm4 + 8.978 cm4
Iox2 = 15.64 cm4

Iox3 = B x H3 /12 + (20cm2)(5.33cm)2
Iox3 = (2cm) x (10cm)3 / 12 + 568.2 cm4
Iox3 = 166.7cm4 + 568.2 cm4
Iox3 = 734.84 cm4

ITOTX = Iox1+Iox2+Iox3
ITOTX= 602.84 cm4 +15.64 cm4 +734.84 cm4
ITOTX=1353.32


Con respecto a Y

Ioy1 = B3 x H /12 + (20cm2)(5.33cm)2
Ioy1 = (2cm)3 x (10cm) /12 + 568.2 cm4
Ioy1 = 6.667 cm4 + 568.2 cm4

Ioy2 = B3 x H /12 + (20cm2)(0.67cm)2
Ioy2 = (10cm)3 x (2cm) /12 + 8.978 cm4
Ioy2 = 166.7 cm4 + 8.978 cm4
Ioy2 = 175.7 cm4

Ioy3= B3 x H /12 + (20cm2)(4.67cm2)
Ioy3 = (2cm)3 x (10cm) /12 + 436.2 cm4
Ioy3 = 6.667 cm4 + 436.2 cm4
Ioy3 = 442.8 cm4

ITOTY = IoY1+IoY2+IoY3
ITOTY= 574.8 cm4 + 175.7 cm4 + 442.8 cm4
ITOTY= 1193 cm4
[*[Ángel Adalberto Gómez Romero]*] GR-081268

Solucion ejercicio uno:

Primero calculamos las areas de cada uno de los rectangulos que forma la figura.

Area 1: bxh=2cmx10cm=20cm^2
Area 2: bxh=10cmx2cm=20cm^2
Area 3: bxh=2cmx10cm=20cm^2

Luego calculamos el centroide de toda la figura sabiendo que el centroide del rectangulo uno (rectangulo superior de la figura) esta en los puntos x=1cm e y=15cm; el centroide del rectangulo dos (rectangulo del centro) esta en los puntos x=7cm e y=11cm; y que el centroide del rectangulo 3 (rectangulo inferior) esta en los puntos x=11cm e y=5cm:

Xc= (20cm^2x1cm)+ (20cm^2x7cm) + (20cm^2x11cm) / 60 cm^2
Xc= 6.333 cm

Yc= (20cm^2x15cm)+ (20cm^2x11cm) + (20cm^2x5cm) / 60 cm^2
Yc= 10.333 cm

Despues de obtener las coordenadas del centroide de toda la figura, se obtiene el momento de inercia de cada uno de los rectangulos con respecto a x y con respecto a y:

Respecto a x:

Iox1= (2cm(10cm)^3/12) + 20cm^2(4.67cm)^2
Iox1= 602.84cm^4

Iox2= (10cm(2cm)^3/12) + 20cm^2(0.67cm)^2
Iox2= 15.64cm^4

Iox3= (2cm(10cm)^3/12) + 20cm^2(5.33cm)^2
Iox3= 734.84cm^4

Respecto a y:

Ioy1= (10cm(2cm^3)/12) + 20cm^2(5.33cm)^2
Ioy1= 574.84cm^4

Ioy2= (2cm(10cm^3)/12) + 20cm^2(0.67cm)^2
Ioy2= 175.64cm^4

Ioy3= (10cm(2cm^3)/12) + 20cm^2(4.67cm)^2
Ioy3= 442.84 cm^4

Por ultimo, despues de haber obtenido los momentos de inercia en cada uno de los rectangulos y en cada eje, se suman para obtener el momento de inercia total en x y en y:

Itotalx= 602.84cm^4 + 15.64cm^4 + 734.84cm^4
Itotalx= 1353.32cm^4

Itotaly= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4
Itotaly= 1193.32cm^4

Jose alexander hernandez velasquez hv080894



las areas de cada uno de los rectangulos.

Area 1: bxh=2cmx10cm
=20cm^2
Area 2: bxh=10cmx2cm
=20cm^2
Area 3: bxh=2cmx10cm
=20cm^2


Xc= (20cm^2x1cm)+ (20cm^2x7cm) + (20cm^2x11cm) / 60 cm^2
Xc= 6.333 cm

Yc= (20cm^2x15cm)+ (20cm^2x11cm) + (20cm^2x5cm) / 60 cm^2
Yc= 10.333 cm

el momento de inercia de cada uno de los rectangulos con respecto a x y con respecto a y:

Respecto a X

Iox1= (2cm(10cm)^3/12) + 20cm^2(4.67cm)^2

Iox1= 602.84cm^4

Iox2= (10cm(2cm)^3/12) + 20cm^2(0.67cm)^2

Iox2= 15.64cm^4

Iox3= (2cm(10cm)^3/12) + 20cm^2(5.33cm)^2

Iox3= 734.84cm^4

Respecto a Y

Ioy1= (10cm(2cm^3)/12) + 20cm^2(5.33cm)^2

Ioy1= 574.84cm^4

Ioy2= (2cm(10cm^3)/12) + 20cm^2(0.67cm)^2

Ioy2= 175.64cm^4

Ioy3= (10cm(2cm^3)/12) + 20cm^2(4.67cm)^2

Ioy3= 442.84 cm^4

los momentos de inercia en cada uno de los rectangulos y en cada eje, se suman para obtener el momento de inercia total en x y en y:

Itotalx= 602.84cm^4 + 15.64cm^4 + 734.84cm^4

Itotalx= 1353.32cm^4

Itotaly= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4

Itotaly= 1193.32cm^4

En primer lugar calculamos el centroide de la figura total.

Datos para resolver el problema.
FiguraFigura1Figura2Figura3

A	X	Y	Dx	Dy

PROBLEMA 1

LOS CENTROIDES....


 Para encontrar los momentos de Inercia decimos que:
Itot= Itot1 + Itot2

Para Ixx tenemos:
Itot1= Iox1 + A*d² = (b)(h)³/12 = (2)(10) ³/12 + (20*4.67²)= 602.84cm⁴
Itot2= Iox2 + A*d² = (b)(h)³/12 = (10)(2) ³/12 + (20*0.67²)= 15.64⁴
Itot3= Iox3 + A*d² = (b)(h)³/12 = (2)(10) ³/12 + (20*(-5.33)²)=734.84cm⁴

 Entonces Ixx:
Ixx =602.84cm⁴ + 15.64cm⁴ + 734.84cm⁴ = 1353cm⁴

Para Iyy tenemos:
Itot1= Ioy1 + A*d² = (h)(b)³/12 = (10)(2)³/12 + (20*(-5.33)²)= 574.84cm⁴
Itot1= Ioy2 + A*d² = (h)(b)³/12 = (2)(10)³/12 + (20*0.67²)= 175.64cm⁴
Itot1= Ioy3 + A*d² = (h)(b)³/12 = (10)(2)³/12 + (20*4.67²)= 442.84cm⁴

Entonces Iyy:
Iyy =574.84cm⁴+ 175.64cm⁴+ 442.84cm⁴=1193.32 cm⁴

LA FIGURA SE DIVIDE EN TRES PARTES

A1 = b*h = 10cm*2cm = 20cm2
A2 = b*h = 10cm*2cm = 20cm2
A3 = b*h = 10cm*2cm = 20cm2
AREA TOTAL = 60cm^2

ENCONTRAMOS EL CENTRO DE CADA UNA DE LAS FIGURAS

PARA EL AREA 1 TENEMOS QUE

X1 = 1cm , Y1 = 15 cm
PARA EL AREA 2 TENEMOS :
X2 = 7 cm , Y2 = 11 cm
PARA EL AREA 3 TENEMOS :
X3 = 11 cm, Y3 = 5 cm

luego calculamos el centroide de toda la figura:

Xc = [(20cm^2)*(1 cm)+(20cm^2)*(7cm)+(20cm^2)*(11cm)]/60cm2
Xc = [20cm3+140cm3+220cm3/60cm2]
Xc = 6.33 cm
Yc= [(20cm^2)*(15cm)+(20cm^2)*(11cm)+(20cm^2)*(5cm)]/60cm2
Yc= 300cm3+220cm3+100cm3/60 cm2
Yc= 620cm3/60 cm2
Yc= 10.33cm

EN ESTAS COORDENADAS ES POR DONDE PASA EL EJE CENTROIDAL DE LA FIGURA
(6.33,10.33)

CALCULANDO EL MOMENTO DE INERCIA DE CADA FIGURA

Ixx=Iox1+Iox2+Iox3
Iox1= [b*h3]/12 + A (d2)     A=20cm2  ,  d=15-10.33=4.67
Iox1= [2*103]/12 + 20cm2*(4.67cm)2
Iox1= 166.67cm4+ 436.18cm4
Iox1= 602.85cm4

Iox2= [b*h3/12 + A (d2) A=20cm2 d=0.67cm
Iox2= 10*23/12 + 20(0.672)
Iox2= 6.67cm4+ 8.98cm4
Iox2= 15.65 cm4

Iox3= [b*h3/12] + A (d2) A=20cm2 d = -5.33cm
Iox3= [2*103/12 + 20cm2(-5.33cm)2
Iox3 = 166.67cm4+568.18cm4
Iox3= 734.85 cm4

Ixx = 602.85cm4+15.65cm4+734.85cm4
Ixx= 1353.35cm4

Iyy = Ioy1+Ioy2+Ioy3

Ioy1= [b3*h/12]+Ad2 d=-5.33cm
Ioy1= [8*10/12]cm4+20cm2*(-5.33cm)2
Ioy1= [6.67cm4+568.18cm4]
Ioy1= 574.85cm4

Ioy2= [b3*h/12]+Ad2
Ioy2= [1000*2/12]cm4+20cm2*(0.67cm)2
Ioy2= [166.67cm4]+8.98cm4
Ioy2= 175.65cm4

Ioy3= [b3*h/12]+Ad2
Ioy3= [8*10]/12 +(20)*(4.67)2
Ioy3= 6.67cm4+436.18cm4
Ioy3= 442.85 cm4

Iyy= 574.85cm4+175.65cm4+442.85cm4
Iyy= 1193.35 cm4

Ixx=1353.35 cm4
Iyy=1193.35 cm4

Primero hay que encontrar el area de cada uno de los rectangulos.

Area 1: b.h=2cm.10cm=20cm^2
Area 2: b.h=10cm.2cm=20cm^2
Area 3: b.h=2cm.10cm=20cm^2

Calculamos el centroide (x,y)

Xc= (20cm^2x1cm)+ (20cm^2x7cm) + (20cm^2x11cm) / 60 cm^2
Xc= 6.333 cm

Yc= (20cm^2x15cm)+ (20cm^2x11cm) + (20cm^2x5cm) / 60 cm^2
Yc= 10.333 cm

Momento de inercia de cada uno de los rectángulos con respecto a X y Y.

Respecto a X
Iox1= (2cm(10cm)^3/12) + 20cm^2(4.67cm)^2
Iox1= 602.84cm^4

Iox2= (10cm(2cm)^3/12) + 20cm^2(0.67cm)^2
Iox2= 15.64cm^4

Iox3= (2cm(10cm)^3/12) + 20cm^2(5.33cm)^2
Iox3= 734.84cm^4

Respecto a Y
Ioy1= (10cm(2cm^3)/12) + 20cm^2(5.33cm)^2
Ioy1= 574.84cm^4

Ioy2= (2cm(10cm^3)/12) + 20cm^2(0.67cm)^2
Ioy2= 175.64cm^4

Ioy3= (10cm(2cm^3)/12) + 20cm^2(4.67cm)^2
Ioy3= 442.84 cm^4

Cada momento de inercia de cada rectángulo se suma en su respectivo eje para asi obtener el momento de inercia total en X y Y.

Itotx= 602.84cm^4 + 15.64cm^4 + 734.84cm^4
Itotx= 1353.32cm^4

Itoty= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4
Itoty= 1193.32cm^4

Problema 1. Rafael efraín Gil Belloso

Primeramente ,la figura se puede descomponer en tres rectangulos, a los cuales se procedra a sacar el area.

Rectangulo 1: Fórmula:B*H (2cm*10cm)= 20cm²
Rectangulo 2: Fórmula: B*H (10cm*2cm)= 20cm²
Rectangulo 3: Formula: B*H (2cm*10cm)= 20cm²

La figura a pesar de no presentar simetria bilateral, si presenta simetria ya que las figuras que quedan a ambos lados al pasar un eje y tienen las mismas dimensiones, pero tienen una orientacion diferente.
Se tiene que:

X1: 1 cm Y1: 15 cm
X2: 7 cm Y2: 11 cm
X3: 11 cm Y3: 5 cm

Centroide en x:
Xc= (20cm²x1cm)+ (20cm²x7cm) + (20cm²x11cm)

60 cm²
Xc= 6.333

Centroide en y:
Yc= 20cm²x15cm)+ (20cm²x11cm) + (20cm²x5cm)

60 cm²
Yc=10.333 cm

Ahora se procedera a encontrar los momentos de inercia de los tres rectangulos en los ejes x e y.

Formula: B*H³/12

En x:

Iox1= (2cm*(10cm) ³ /12) + 20cm² (4.67cm) ²
Iox1= 602.84cm^4

Iox2= (10cm*(2cm) ³ /12) + 20cm² (0.67cm) ²
Iox2= 15.64cm^4

Iox3= (2cm*(10cm) ³ /12) + 20cm² (5.33cm) ²
Iox3= 734.84cm^4

En y:

Ioy1= (10cm*(2cm) ³/12) + 20cm^2(5.33cm)^2
Ioy1= 574.84cm^4

Ioy2= (2cm*(10cm) ³/12) + 20cm^2(0.67cm)^2
Ioy2= 175.64cm^4

Ioy3= (10cm*(2cm)³/12) + 20cm^2(4.67cm)^2
Ioy3= 442.84 cm^4


Ahora se calulan los momentos de inercia total:

Itotalx= 602.84cm^4 + 15.64cm^4 + 734.84cm^4
Itotalx= 1353.32cm^4

Itotaly= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4
Itotaly= 1193.32cm^4

En primer lugar calculamos el centroide de la figura total.

Datos para resolver el problema.

Figura|Area(cm^2)|X|Y|Dist.X|Dist.Y|
Figura1 20 1 15 4.67 -5.33
Figura2 20 7 11 0.67 0.67
Figura3 20 11 5 -5.33 4.67



Como primer punto para el calculo del centroide necesitamos el valor de las areas respectivas...
Referencias:
Calculo de las areas.
A1=b*h A2=b*h A3=(b*h)
A1=(2)(10) A2=(10)(2) A3=(2)(10)
A1=20cm^2 A2=20cm^2 A3=20cm^2

At=sumatoria de todas las areas.
At=20*3
At=60cm^2

Calculo de las coordenadas del centroide.

Xc=[(A1)(X1)+(A2)(X2)+(A3)(X3)]/At
Xc=[(20)(1)+(20)(7)+(20)(11)]/60
Xc=6.33


Yc=[(A1)(Y1)+(A2)(Y2)+(A3)(Y3)]/At
Yc=[(20)(15)+(20)(11)+(20)(5)]/60
Yc=10.33

Esto nos da que nuestro centroide "C" se encuentra en C(6.33,10.33)

Ahora colocamos nuestra XX y YY en los ejes centroidales.....
En cuanto el valor de inercia en XX
Itx=Sumatoria de Ix
Itx= (b1(h1)^3/12) + A1(dx1)^2+(b2(h2)^3/12) + A2(dx2)^2)+(b2(h2)^3/12) + A2(dx2)^2
Itx= (2cm(10cm)^3/12) + 20cm(4.67cm)^2+(10cm(2cm)^3/12) + 20cm(0.67cm)^2+(2cm(10cm)^3/12) + 20cm(5.33cm)^2
Itxx=1353.35cm^4


En cuanto el valor de inercia en YY
Ity=Sumatoria de Iy
Itx= (b1(h1)^3/12) + A1(yx1)^2+(b2(h2)^3/12) + A2(dy2)^2)+(b2(h2)^3/12) + A2(dy2)^2
Itx= (10cm(2cm)^3/12) + 20cm(-5.33)^2+(2cm(10cm)^3/12) + 20cm(0.67cm)^2+(10cm(2cm)^3/12) + 20cm(4.67cm)^2
Itxx=1193.35cm^4




BUeno pues ing con esto despido ya estuvo bastante larga la jornada de ahora espero haberla resuleto bien cuidece pase una linda noche!!!

P.D. Notara q es casi el mismo formato que para mi segunda respuesta solo cambie algunas cosas ojo q copie de mi mismo trabajo y eso no dijo que no se pudiera!!!! jajajaj solo como aclaracion por si acaso

Calculamos las áreas.
A1: b x h = (2cm) x (10cm) = 20cm^2
A2: b x h = (10cm) x (2cm) = 20cm^2
A3: b x h = (2cm) x (10cm) = 20cm^2

Posición de los Centroides de cada pieza
A1: x = 1cm e y = 15cm
A2: x = 7cm e y = 11cm
A3: x = 11cm e y = 5cm:

Obtención del centriode de toda la figura:
Xc = ( ( (20cm^2) x (1cm) ) + ( (20cm^2) x (7cm) ) + ( (20cm^2) x (11cm) ) ) / 60cm^2
Xc = 6.33 cm

Yc = ( ( (20cm^2) x (15cm) ) + ( (20cm^2) x (11cm) ) + ( (20cm^2) x (5cm) ) ) / 60cm^2
Yc = 10.33 cm

Momentos de Inercia.
Con respecto al eje x:

Iox1 = ( (2cm) x ( (10cm)^3) ) / 12 ) + ( (20cm^2) x ( (4.67cm)^2)
Iox1 = 602.84cm^4

Iox2= ( (10cm) x ( (2cm)^3) ) / 12) + ( (20cm^2) x ( (0.67cm)^2)
Iox2= 15.64cm^4

Iox3= ( (2cm) x ( (10cm)^3) ) / 12) + ( (20cm^2) x ( (5.33cm)^2)
Iox3= 734.84cm^4

Respecto a y:

Ioy1= ( (10cm) x ( (2cm)^3 ) / 12) + ( (20cm^2) x ( (5.33cm)^2)
Ioy1= 574.84cm^4

Ioy2 = ( (2cm) x ( (10cm)^3) / 12) + ( (20cm^2) x ( (0.67cm)^2)
Ioy2 = 175.64cm^4

Ioy3 = ( (10cm) x ( (2cm)^3) / 12) + ( (20cm^2) x ( (4.67cm)^2)
Ioy3 = 442.84cm^4

Obteniendo Momento de Inercia Total.
Itotalx = 602.84cm^4 + 15.64cm^4 + 734.84cm^4
Itotalx = 1353.32cm^4

Itotaly = 574.84cm^4 + 175.64cm^4 + 442.84cm^4
Itotaly = 1193.32cm^4

Luís Fidel Aguirre Hernández AH081164

Para comenzar a encontrar los momentos de inercia Ixx, Iyy
Primero se tienen que conocer las áreas de los rectángulos que en este caso serian:

Primera área: b*h = (2cm)* (10cm) = 20cm²
Segunda área: b*h = (10cm)* (2cm) = 20cm²
Tercera área 3: b*h = (2cm)* (10cm) = 20cm²

Ahora el centroide x,y


Xc= (20cm²)*(1cm)+ (20cm²)*(7cm) + (20cm²)*(11) / 60 cm²
Xc = 380 cm3 /60 cm² Xc= 6.33 cm


Yc = (20cm²)*(15cm) + (20cm²)*(11cm) + (20cm²)*(5cm) / 60cm²
Yc =620 cm3 / 60cm² Yc =10.33 cm

Ahora se encuentra el momento de inercia en cada uno de los rectángulos con respecto a X y Y.

Con respecto a X tenemos:
Iox1= (2cm (10cm) ^3/12) + 20cm² (4.67cm) ²

Iox1= 602.84cm^4

Iox2= (10cm (2cm) ^3/12) + 20cm² (0.67cm) ²

Iox2= 15.64cm^4

Iox3= (2cm (10cm) ^3/12) + 20cm² (5.33cm) ²

Iox3= 734.84cm^4

ITOTX = Iox1+Iox2+Iox3
ITOTX= 602.84 cm4 +15.64 cm4 +734.84 cm4

ITOTX=1353.32



Con respecto a Y
Ioy1= (10cm(2cm^3)/12) + 20cm² (5.33cm) ²

Ioy1= 574.84cm^4

Ioy2= (2cm(10cm^3)/12) + 20cm² (0.67cm) ²

Ioy2= 175.64cm^4

Ioy3= (10cm(2cm^3)/12) + 20cm² (4.67cm) ²

Ioy3= 442.84 cm^4
Itoty= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4

ITOTY= 1193.32CM^4

Calculando cada una de las areas:

Area 1: bxh = ( 2cm )( 10cm ) = 20cm^2
Area 2: bxh = ( 10cm )( 2cm ) = 20cm^2
Area 3: bxh = ( 2cm )( 10cm ) = 20cm^2


Puntos del centroide para cada rectángulo:

Rectángulo 1: x=1cm e y=15cm
Rectángulo 2: x=7cm e y=11cm
Rectángulo 3: x=11cm e y=5cm

Xc = ( 20cm^2 )( 1cm ) + ( 20cm^2 )( 7cm ) + ( 20cm^2 )( 11cm ) / 60 cm^2
Xc = 6.333 cm

Yc= ( 20cm^2 )( 15cm ) + ( 20cm^2 )( 11cm ) + ( 20cm^2 )( 5cm ) / 60 cm^2
Yc= 10.333 cm

Obteniendo el Momento de Inercia respectos a los ejes para cada rectangulo:

Respecto al eje X:

Iox1= (2cm(10cm)^3/12) + 20cm^2(4.67cm)^2
Iox1= 602.84cm^4

Iox2= (10cm(2cm)^3/12) + 20cm^2(0.67cm)^2
Iox2= 15.64cm^4

Iox3= (2cm(10cm)^3/12) + 20cm^2(5.33cm)^2
Iox3= 734.84cm^4

Respecto al eje Y:

Ioy1= (10cm(2cm^3)/12) + 20cm^2(5.33cm)^2
Ioy1= 574.84cm^4

Ioy2= (2cm(10cm^3)/12) + 20cm^2(0.67cm)^2
Ioy2= 175.64cm^4

Ioy3= (10cm(2cm^3)/12) + 20cm^2(4.67cm)^2
Ioy3= 442.84 cm^4

Obteniendo la Inercia total en cada eje:

Para eje X:

ItotalX= 602.84cm^4 + 15.64cm^4 + 734.84cm^4
ItotalX= 1353.32cm^4

Para eje Y:

ItotalY= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4
ItotalY= 1193.32cm^4

Primero debemos encontrar el area de cada rectangulo:

A1: b.h=2cm.10cm=20cm^2
A2: b.h=10cm.2cm=20cm^2
A3: b.h=2cm.10cm=20cm^2

Calculamos los centroides

Xc= (20cm^2x1cm)+ (20cm^2x7cm) + (20cm^2x11cm) / 60 cm^2
Xc= 6.333 cm

Yc= (20cm^2x15cm)+ (20cm^2x11cm) + (20cm^2x5cm) / 60 cm^2
Yc= 10.333 cm

Momento de inercia de cada uno de los rectángulos con respecto a X y Y.

Respecto a X
Iox1= (2cm(10cm)^3/12) + 20cm^2(4.67cm)^2
Iox1= 602.84cm^4

Iox2= (10cm(2cm)^3/12) + 20cm^2(0.67cm)^2
Iox2= 15.64cm^4

Iox3= (2cm(10cm)^3/12) + 20cm^2(5.33cm)^2
Iox3= 734.84cm^4

Respecto a Y
Ioy1= (10cm(2cm^3)/12) + 20cm^2(5.33cm)^2
Ioy1= 574.84cm^4

Ioy2= (2cm(10cm^3)/12) + 20cm^2(0.67cm)^2
Ioy2= 175.64cm^4

Ioy3= (10cm(2cm^3)/12) + 20cm^2(4.67cm)^2
Ioy3= 442.84 cm^4

Cada momento de inercia de cada rectángulo se suma en su respectivo eje para asi obtener el momento de inercia total en X y Y.

Itotx= 602.84cm^4 + 15.64cm^4 + 734.84cm^4
Itotx= 1353.32cm^4

Itoty= 574.84cm^4 + 175.64cm^4 + 442.84 cm^4
Itoty= 1193.32cm^4

Alicia Maricelle Marroquín Girón MG080846
Primero visualizamos a cuanto es que vamos a dividir la figura en este caso seria en 3, estos serian todos rectangulos asi que apartir de la tabla podemos decir que:

	A	X	Y	dx	dy
I	20cm^2	1cm	15cm	-4.67cm	5.33cm
II	20cm^2	7cm	11cm	0.67cm	0.67cm
III	20cm^2	11cm	5cm	5.33cm	-4.67cm

Xc= ((20cm^2)(1cm)+(20cm^2)(7cm)+(20cm^2)(11cm))/(60cm^2)
Xc= (380cm^3)/(60cm^2)= 6.33cm

Yc= ((20cm^2)(15cm)+(11cm^2)(7cm)+(20cm^2)(5cm))/(60cm^2)
Yc= (620cm^3)/(60cm^2)= 10.33cm

Momentos de inercia!!

Ixx= Iox1 + Iox2 + Iox3

Iox=bh^3/12 +Ad^2

Iox1= bh^3/12 +Ad^2
Iox1= 2cm(10cm^3)/12 +20cm^2(-4.67cm)^2
Iox1=602.85 cm^4

Iox2= bh^3/12 +Ad^2
Iox2= 10cm(2cm^3)/12 +20cm^2(0.67cm)^2
Iox2= 15.65 cm^4

Iox3= bh^3/12 +Ad^2
Iox3= 2cm(10cm^3)/12 +20cm^2(5.33cm)^2
Iox3=734.85 cm^4

Ixx= Iox1 + Iox2 + Iox3
Ixx= 602.85cm^4 + 15.65 cm^4 + 734.85 cm^4
Ixx=1353.35 cm^4


Iyy= Ioy1 + Ioy2 + Ioy3

Ioy=bh^3/12 +Ad^2

Ioy1= bh^3/12 +Ad^2
Ioy1= 10cm(2cm^3)/12 +20cm^2(5.33cm)^2
Ioy1=574.85 cm^4

Ioy2= bh^3/12 +Ad^2
Ioy2= 2cm(10cm^3)/12 +20cm^2(0.67cm)^2
Ioy2= 175.65 cm^4

Ioy3= bh^3/12 +Ad^2
Ioy3= 10cm(2cm^3)/12 +20cm^2(4.67cm)^2
Ioy3= 442.87 cm^4

Iyy= Ioy1 + Ioy2 + Ioy3
Iyy= 574.85 cm^4 + 175.65 cm^4 + 442.87 cm^4
Iyy=1193.37 cm^4

Mi primera respuesta ing. perdon la tardanza pero costo subir las imagenes!

Perdon falto una profe! XD es la 2º imagen despues del diagrama jeje sorry!

muy buenas noches ingeniero.
aqui esta la primera respuesta:
pimero dividimos la pieza en figuras mas simples y despues encontramos los centroides de cada figura ubicando todo en un eje de coordenadas. despues de encontrar el centroide de toda la pieza (Xc, YC) se colocara Xc y Yc como nuevo eje de coordenadas:



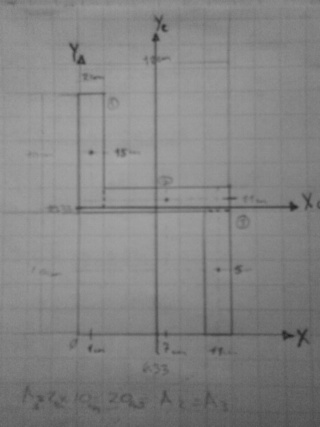
hallamos el centroide de toda la pieza para ubicar el eje Xc y el eje Yc, para ello nos auxiliamos de un cuadro:



Ahora encontramos el momento de inercia tanto en x como en y, primero en Ixx:



Ixx= 1353.32cm^4
y luego en Iyy:



Iyy=1193.32cm^4

JORGE LUIS SANCHEZ AGUILAR
SA070964

Que tal ingeniero? Aqui le mando la respuesta al problema uno, algo largo pero me llegan estos problemas asi: largos pero entendibles.

AREA X Y DX DY
1 20cm2 1cm 15cm 4.67cm 5.33cm
2 20cm2 7cm 11cm 0.67cm 0.67cm
3 20cm2 11cm 5cm 5.33cm 4.67cm


Area 1 = B x H
Area 1 = (2cm)(10cm)
Area 1= 20cm2

Area 2= B x H
Area 2= (10cm)(2cm)
Area 2= 20cm2

Area 3 = B x H
Area 3 = (2cm)(10cm)
Area 3= 20 cm2

Xc= (20cm2)(1cm)+ (20cm2)(7cm) + (20cm2)(11) / 60 cm2
Xc = 380 cm3 /60 cm2
Xc= 6.33 cm

Yc = (20cm2)(15cm) + (20cm2)(11cm) + (20cm2)(5cm) / 60cm2
Yc =620 cm3 / 60cm2
Yc =10.33 cm


Iox1 = B x H3 / 12 + (20cm2)(4.67cm)2
Iox1 = (2cm) x (10cm)3 /12 + 436.2 cm4
Iox1 = 166.7 cm4 + 436.2 cm4
Iox1 = 602.9 cm4

Iox2 = B x H3 /12 + (20cm2)(0.67cm)2
Iox2 = (10cm) x (2cm)3 /12 + 8.978 cm4
Iox2 = 6.667 cm4 + 8.978 cm4
Iox2 = 15.65 cm4

Iox3 = B x H3 /12 + (20cm2)(5.33cm)2
Iox3 = (2cm) x (10cm)3 / 12 + 568.2 cm4
Iox3 = 166.7cm4 + 568.2 cm4
Iox3 = 734.9 cm4

Ioxtotal: Iox1 + Iox2 + Iox3
Ioxtotal: 602.9cm4 + 15.65 cm4 + 734.9 cm4
Ioxtotal: 1353 cm4

Ioy1 = B3 x H /12 + (20cm2)(5.33cm)2
Ioy1 = (2cm)3 x (10cm) /12 + 568.2 cm4
Ioy1 = 6.667 cm4 + 568.2 cm4

Ioy2 = B3 x H /12 + (20cm2)(0.67cm)2
Ioy2 = (10cm)3 x (2cm) /12 + 8.978 cm4
Ioy2 = 166.7 cm4 + 8.978 cm4
Ioy2 = 175.7 cm4

Ioy3= B3 x H /12 + (20cm2)(4.67cm2)
Ioy3 = (2cm)3 x (10cm) /12 + 436.2 cm4
Ioy3 = 6.667 cm4 + 436.2 cm4
Ioy3 = 442.8 cm4

Ioytotal = Ioy1 + Ioy2 + Ioy3
Ioytotal = 574.8 cm4 + 175.7 cm4 + 442.8 cm4
Ioytotal = 1193 cm4


Eje en x = 6.33cm
Eje en y = 10.33cm