PROBLEMA 02

BUENOS DIAS INGENIERO COMO ESTAMOS, AQUI LE PRESENTO EL DESARROLLO DEL PROBLEMA NUMERO 2 (AL PELO)

PRIMERAMENTE SE PONE EL SISTEMA EN UN PLANO


SEGUNDO PASO

COMO YA TENEMOS LOS DIAMETROS DE LOS REMACHES PASAREMOS A CALCULAR EL AREA DE CADA UNO



PODEMOS VER CLARAMENTE QUE
A1=A2=A5=A6 Y QUE A3=A4

ENTONCES -----> A1= π(r^2)
r=d1/2
r=4/2 ---------> r=2
A1=(3.1416)(2^2)
A1=12.5664

A3=π(r^2)
r=d3/2
r=8/2
r=4
A3=(3.1416)(4^2)
A3=50.2656
-------------------------------------------------------------
A1=12.5664
A2=12.5664
A3=50.2656
A4=50.2656
A5=12.5664
A6=12.5664

AT=A1+A2+A3A+A4+A5+A6
AT=150.7968
----------------------------------------------------------------
AHORA BASANDONOS EN NUESTRO PLANO DE COORDENADAS LOS PUNTOS EN X y en Y

X1= 0
X2= 20
X3= 40
X4= 10
X5= 30
X6= 20

Y1= 40
Y2= 40
Y3= 40
Y4= 20
Y5= 20
Y6= 0
--------------------------------------------------------------------------
LUEGO DE ESTO PASAMOS AL PLANTEAMIENTO DE LAS ECUACIONES:

DONDE AT ES EL AREA TOTAL DE LA FIGURA

X=(X1A1+X2A2+X3A3+X4A4+X5A5+X6A6) / (AT)
Y=(Y1A1+Y2A2+Y3A3+Y4A4+Y5A5+Y6A6) / (AT)

COORDENADAS CENTROIDE = X,Y

AHORA PONGAMOLE NUMEROS

X=[(0)(12.5664) + (20)(12.5664) + 40(50.2656) + (10)(50.2656) + (30)(12.5664) + (20)(12.5664)] / [150.7968]

X=[0 + 251.328 + 2010.624 + 502.656 + 376.992 + 251.328]/150.7968



Y=[(40)(12.5664) + (40)(12.5664) + (40)(50.2656) + (20)(50.2656) + (20)(12.5664) + (0)(12.5664)] / [150.7968]

Y= [502.656 + 502.656 + 2010.624 + 1005.312 + 251.328 + 0] / [150.7968]



RESPUESTA-----> CENTROIDE = 22.5x, 28.33y

ingeniero aqui va el problema numero 2

trabajando en grupo JORGE LUIS SANCHEZ AGUILAR y JORGE ALBERTO SOLORZANO VALDES

BUENO...AQUI VAMOS

como primer paso escogimos esta forma de presentar en el eje (y) y (x) el problema:




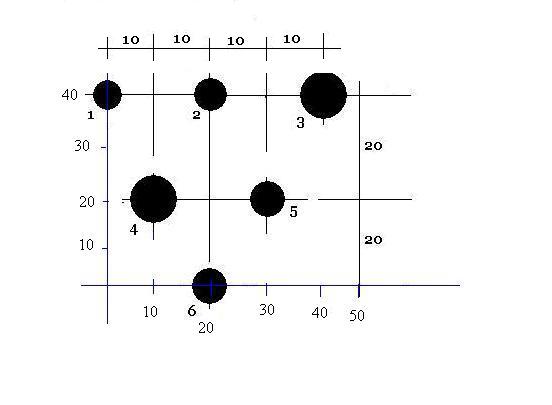
por simple inspeccion podemor deducir ciertas cosas que nos ayudaran a solucionar este problema:

1- las Figuras A1, A2, A5 y A6 son iguales en vista de como estan en la imagen dada y
2- las Figuras A3 y A4 son iguales en vista de como estan en la imagen dada.

ahora:

como estas figuras son iguales sacaremos 2 areas y despues solo les pondremos los valores a las que sean iguales:

A2= π(r^2)
A2=(3.1416)(2^2)
A2=12.56
****************
A4= π(r^2)
A4=(3.1416)(4^2)
A4=50.26
****************

Xenia Lissette Cortez Nataren CN071387
Jose Guillermo Antonio Figueroa Henriquez FH080737

Muy buenos dias ing. por aqui disculpas de la foto q se ve algo mal pero tube problemitas con mi cam

y al fin luego del desayuno merecido termino el ejercicio jaja
herberth gonzalez
allan estrada
samuel angulo

continuacion de la Respuesta:

con las areas encontradas y con los puntos que pusimos acerca de la igualdad de las figuras tenemos ya todas las areas de las figuras que aparecen en la imagen:

*A1=12.56
*A2=12.56
*A3=50.26
*A4=50.26
*A5=12.56
*A6=12.56

ahora, con las areas que tenemos encontramos la area total de la figura principal:

AreaTotal = A1+A2+A3+A4+A5+A6
AreaTotal = (12.56*4)+ (50.26*2)
AreaTotal = 50.24+100.52
AreaTotal = 150.76

**************************************************************

ahora sacamos los puntos coordenados de la Figuras las cuales pusimos en la imagen en la cual posicionamos en el eje coordenado

continuacion de la Respuesta:

ahora sacamos los puntos coordenados de la Figuras las cuales pusimos en la imagen en la cual posicionamos en el eje coordenado:

A1------ X=0
Y=40

A2------X=20
y=40

A3------X=40
Y=40

A4------X=40
Y=20

A5------X=30
Y=20

A6------X=20
Y=20

YA CASI...................

RONALD BENJAMIN RAMOS PUTUN Y GASPAR ALFREDO PEREZ MAGAÑA

Primeramente el Area 1 , 2 , 5 y 6 seran las mismas y tambien el radio.

[b] Radio: r = d/2
r = 4 cm / 2 = 2 cm

Area circulo 1, 2, 5 y 6
a = (π)(r)^2
a = (3.1416)(2cm)^2
a= 12.5666 cm^2
Radio circulos 3 y 4.

r= d/2
r = 8 cm/ 2 = 4cm

Area circulo 3 y 4
a= (π)(r)^2
a= (3.1416)(8cm)^2
a= 50.2654 cm^2

Coordenadas	Eje X	Eje Y
1	0	40
2	20	40
3	40	40
4	10	20
5	30	20
6	20	0

Centroide en X:

X = (a1)(x1)+(a2)(x2)+(a3)(x3)+(a4)(x4)+(a5)(x5)+(a6)(x6) / a total

x= (12.5666cm^2)(0)+(12.5666cm^2)(20)+(50.2654cm^2)(40)+(50.2654cm^2)(10)+(12.5666cm^2)(30)
+(12.5666cm^2)(20) / 150.7972 cm^2

X= 22.51


Centroide en Y

Y= (a1)(y1)+(a2)(y2)+(a3)(y3)+(a4)(y4)+(a5)(y5)+(a6)(y6) / a total

Y= (12.5666cm^2)(40)+(12.5666cm^2)(40)+(50.2654cm^2)(40)+(50.2654cm^2)(20)+(12.5666cm^2)(20)
+(12.5666cm^2)(0) / 150.7972 cm^2

Y= 28.33

continuacion de la Respuesta: (POR FIN LA ULTIMA PARTE )

Ya teniendo los puntos coordenados de las figuras tanto en X como en Y solo utilizamos la formula para encontrar la componente en Xtotal y la Ytotal:

*formula*
para X:
Xtotal=(X1A1+X2A2+X3A3+X4A4+X5A5+X6A6) / (ATtotal)
Para Y:
Ytotal=(Y1A1+Y2A2+Y3A3+Y4A4+Y5A5+Y6A6) / (ATotal)

por lo que solo poniendo los valores encontrados tenemos:

Xtotal=[(0)(12.56) + (20)(12.56) + 40(50.26) + (10)(50.26) + (30)(12.56) + (20)(12.56)] / [150.76]
Xtotal=[251.2+2010.4+502.6+376.8+251.2] / [150.76]
Xtotal=22.50

Ytotal=[(40)(12.56) + (40)(12.56) + (40)(50.26) + (20)(50.26) + (20)(12.56) + (0)(12.56)] / [150.76]
Ytotal=[502.4+502.4+2090.4+1005.2+251.2] / [150.76]
Ytotal=28.86

bueno ingeniero...que tenga buen domingo...

recordandole que trabajomos en la resolucion de los problemas JORGE LUIS SANCHEZ AGUILAR y JORGE ALBERTO SOLORZANO VALDES


Saluuuuuuuuuuuuu

Primero sacamos los centroides individuales:


Luego calculamos las coordenadas del centroide de todo el conjunto:

bueno profe aqui le va el último espero y este correcto.
PD: antes de cualquier onda pues hay disculpe profe que las respuestas que le mande no se las mande tan explicadas y animadas con dibujos y etc etc, pero como usted sabe estamos corto de tiempo más yo que hahahaha aun estoy secando el teclado, ni modo...

Por simple inspección podemos determinar que A1=A2=A5=A6 y que A3=A4, por lo cual con resolver una de cada de los grupos de áreas estaremos obteniendo el de los demás.

^ = potencia
A1 = π (r^2) r=diámetro/2 r=4/2 r=2
A1 = (3.1416)(2^2)
A1 = 12.56

A3 = π (r^2) r = diámetro/2 r=8/2 r=4
A3=(3.1416)(4^2)
A3=50.26


A1 ^A2 =12.56
A3 ^A4 =50.26
A5 ^ A6=12.56

AT=A1+A2+A3A+A4+A5+A6
AT=150.7968

Según X y Y determinamos:

X1= 0
X2= 20
X3= 40
X4= 10
X5= 30
X6= 20

Y1= 40
Y2= 40
Y3= 40
Y4= 20
Y5= 20
Y6= 0

X= (X1A1+X2A2+X3A3+X4A4+X5A5+X6A6)
AT
Y= Y1A1+Y2A2+Y3A3+Y4A4+Y5A5+Y6A6)
AT


X= (0)(12.56) + (20)(12.56) + 40(50.26) + (10)(50.26) + (30)(12.56) + (20)(12.56)
150.79

X= (0 + 251.32 + 2010.62 + 502.656 + 376.99 + 251.32)
150.79

X=22.5


Y= (40)(12.56) + (40)(12.56) + (40)(50.26) + (20)(50.26) + (20)(12.56)+(0)(12.56)
150.79

Y= (502.65 + 502.65 + 2010.62 + 1005.31 + 251.32 + 0)
150.79

y=28.33



x=22.5
y=28.33