PROBLEMA 01

SOLO UNA PREGUNTA RAPIDA, usted digame si SI o si NO


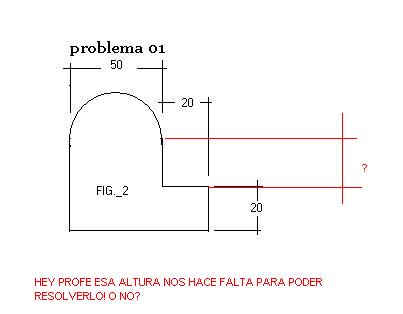
Ya intente analizarlo de diferentes maneras, pero no hayo la manera de que el ejercicio pueda ser resuelto sin esa altura ! PERO BUENO AHI SI NOS PUEDE SEÑALAR ALGUN ASPECTO QUE ESTAMOS OBVIANDO SERIA DE GRAN AYUDA

Buenos dias ingeniero...

fijese que viendo este ejercicio tengo la misma duda que joseph....me parece que necesitamos la magnitud que joseph mostro en su imagen por que sino no hay forma de hallar el area de esta figura y por tanto....segun veo no podriamos seguir con este problema....o si se puede ingeniero....tal vez se me esta escapando algo...


saludos

Como siempre, hay que ubicar la figura en un plano de coordenadas cartesianas



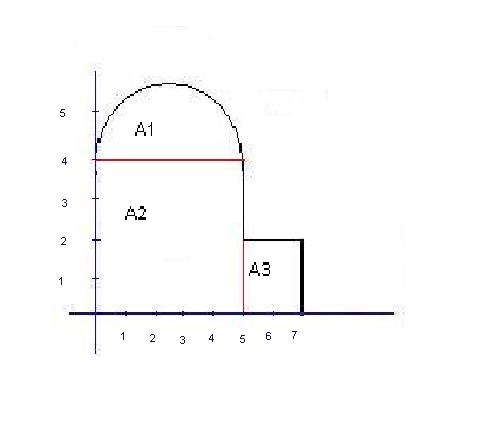
UNA VEZ SE HA REALIZADO ESTO PROCEDEREMOS AL CALCULO DE SUS AREAS

SEMICIRCULO (A1)----------> [π(r^2)]/2--->981.75
RECTANGULO (A2)-----------> b*h--------->2000
CUADRADO (A3)-------------> L*L---------->400

AT=A1+A2+A3= 3381.75


CENTRO DEL SMICIRCULO
X1= d/2--> 5/2 --->2.5
y1= (4r)/3π----->10/9.4248------>1.06--->Y= 4+(1.06)---->Y= 5.06

CENTRO DEL RECTANGULO

X2 = b/2----> 5/2----> 2.5
Y2 = h/2----> 4/2---->2

CENTRO DEL CUADRADO

X3 = L/2------> 2/2---->1
Y3 = L/2-----> 2/2------>1


APLICAREMOSLA FORMULA

X= (A1X1 + A2X2 + A3X3)/AT

X = [(981.75)(2.5) + (2000)(2.5) + (400)(1)] / [3381.75]



Y= [(Y1A1 + Y2A2 +Y3A3)]/[3381.75]
Y= [(5.06)(981.75) + (2)(2000) + (1)(400)] / [3381.75]


respuesta EL CENTROIDE ES: 2.204x, 2.77y

AL UBICAR LA FIGURA EN EL PLANO DE COORDENADAS, LLEGUE A LA CONCLUSION DE QUE LA ALTURA SOBRE LA CUAL PREGUNTABA EN EL PRIMER POST ES IGUAL A 20

Respuesta

Primero como referencia yo tome como Area 1 al semicirculo, de Area 2 rectangulo y como 3 area al cuadrado.

	Area (mm^2)	X	Y
1	981.74	25	50.61
2	2000	25	20
3	400	10	10

Area de Semicirculo :
πr^2/ 2 = π(25mm)^2 / 2 = 981.74 mm^2

Punto en X = 25 mm
Punto en Y = 40 + 4π/3π = 4(25mm)/3(3.1416) = 10.61 mm = 50.61 mm


Area de Rectangulo:
B x H = 50mm * 40 mm = 2000 mm^2

Punto en X = 25 mm
Punto en y = 20 mm

Cuadrado area:

L x L = 20mm * 20mm = 400 mm^2

Punto en X = 10 mm
Punto en y = 10 mm

CENTROIDE EN LA COORDENADA X :

X= ((A1)(X1)+(A2)(X2)+(A3)(X3) )/ Atotal

X= (981.74mm^2)(25mm) + (2000mm^2)(25)+(400mm^2)(10) / 3381.74 mm

X= 23.22 mm

CENTROIDE EN LA COORDENADA Y:

Y = (A1)(Y1)+ (A2)(Y2) + (A3)(Y3) / Atotal

Y = (981.74mm^2)(50.61mm) + (2000mm^2)(20mm) + (400mm^2)(10) / 3381.74 mm

Y = 27.70 mm


Pasando las coordenadas a Cm

Coordenada en X = 2.32 cm
Coordenada en Y = 2.77cm[b][b]

Primero sacamos los centroides de las figuras individuales:


El centroide del semicírculo:


Luego calculamos las coordenadas del centroide de toda la figura:

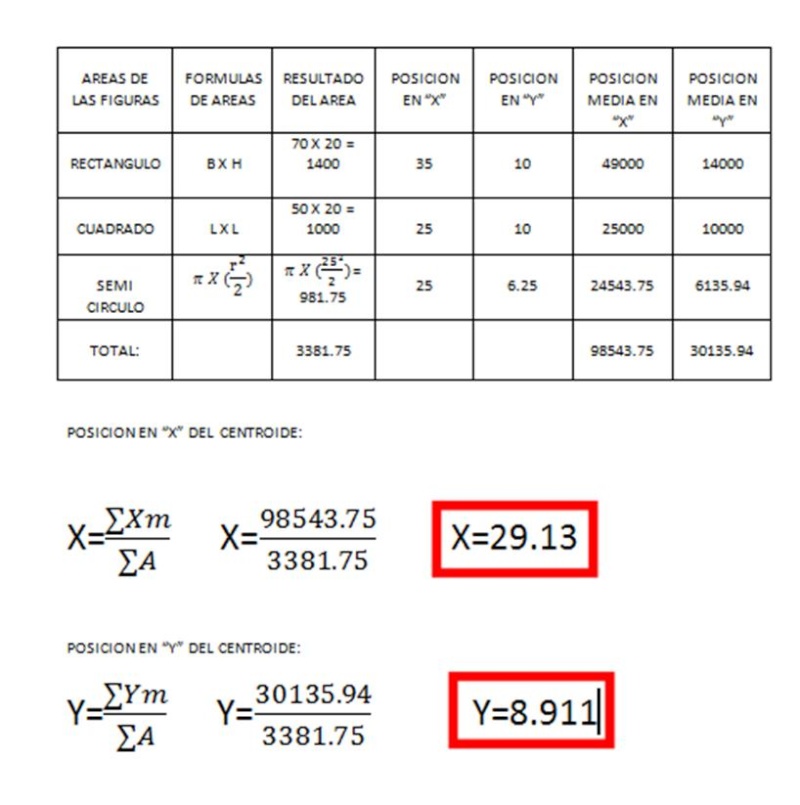
va ps vamos con el primer ejercicio ING. este cafecito y esta semitona mieluda ya me desperto jaja va ps ya subo el otro ahh por cierto realizado por:

samuel angulo
allan estrada
herberth gonzalez

Lo vuelvo a publicar porque en el anterior habia tomado la altura como 30...

Primero sacamos los centroides de las figuras individuales:


El centroide del semicírculo:



Luego calculamos las coordenadas del centroide de toda la figura:

Buenos dias ingeniero aqui le subimos ya el problema uno...trabadando en grupo con Jorge Valdes y Jorge Luis Sanchez Aguilar.

PONIENDO EN PLANO CARTESIANO







LAS COORDENADAS DEL CENTROIDE SON:
2,204X, 2.77Y

INGENIERO PARECE QUE TUVIMOS UN PROBLEMA CON LA IMAGEN DEL PRIMER EJERCICIO, PERO AQUI SE LA MANDAMOS DE NUEVO....JORGE VALDES Y JORGE SANCHEZ

Area de Rectangulo:
B x H = 50mm x 40 mm = 2000 mm^2=

Cuadrado area:

L x L = 20mm x 20mm = 400 mm^2

CENTROIDE EN LA COORDENADA X :

X= ((A1)(X1)+(A2)(X2)+(A3)(X3) )/ Atotal

X= (981.74mm^2)(25mm) + (2000mm^2)(25)+(400mm^2)(10) / 3381.74 mm

X= 23.22 mm

CENTROIDE EN LA COORDENADA Y:

Y = (A1)(Y1)+ (A2)(Y2) + (A3)(Y3) / Atotal

Y = (981.74mm^2)(50.61mm) + (2000mm^2)(20mm) + (400mm^2)(10) / 3381.74 mm

Y = 27.70 mm

Respuesta final en cordenadas en x y en y en cm.

Coordenada en X = 2.32 cm
Coordenada en Y = 2.77cm

PROFE ANTE TODO DISCULPE LA HORA DE SUBIR LAS RESPUESTAS PERO HASTA ESTE MOMENTO ME PUDE CONECTAR YA QUE UNA PERSONA MUY QUERIDA MIA VINO DE GRACIOSA Y PUES POR ACCIDENTE ARROJO UN POQUITITOTE DE AGUA SOBRE EL TECLADO DE MI LAPTOP Y PUES ME ENCONTRABA SECANDOLA CON LA SECADORA DE MI MAMÁ... ¡QUE INGENIOSO NO!?

así esta conformado el grupo:
José Thomas Navas Barrientos NB070928
Neil Sean Guardado Agreda GA060514
Tonatiuh Alexander Paz Hernandez PH060785

A1= semicírculo; A2 = rectángulo; A3 = cuadrado
A1 = [π(r^2)]/2 = 981.75
A2 = b*h = 2000
A3 = L*L = 400

Área del Semicírculo :

Punto X = 25
Punto Y = 40 + 4π/3π = 4(25)/3(3.1416) = 10.61 = 50.61


Área del Rectángulo:

Punto en X = 25
Punto en y = 20

Área del Cuadrado:

Punto en X = 10
Punto en y = 10

CENTROIDE EN LA COORDENADA X :

X= (A1)(X1)+(A2)(X2)+(A3)(X3)
Atotal


X= (981.74^2)(25) + (2000^2)(25)+(400^2)(10)
3381.74

X= 23.22


CENTROIDE EN LA COORDENADA Y:

Y = (A1)(Y1)+ (A2)(Y2) + (A3)(Y3)
Atotal

Y = (981.74^2)(50.61) + (2000^2)(20) + (400^2)(10)
3381.74

Y = 27.70 mm


Pasando las coordenadas a Cm

Coordenada en X = 23.22 o 2.32
Coordenada en Y = 27.70 o 2.77 (dependiendo de las unidades que utilizemos mm o cm)

Xenia Lissete cortez Nataren
Jose Guillermo Antonio Figueroa Henriquez FH080737

Ing mire, yo plantee el problema de otra manera..osea la altura de 20 a la q usted se refiere, yo la plantee que era de 25...pero todo lo demas sta bueno, los procedimientos y todo....

Respuesta

Primero como referencia yo tome como Area 1 al semicirculo, de Area 2 rectangulo y como 3 area al cuadrado.

	Area (mm^2)	X	Y
1	981.74	25	50.61
2	2000	25	20
3	400	60	10

Area de Semicirculo :
πr^2/ 2 = π(25mm)^2 / 2 = 981.74 mm^2

Punto en X = 25 mm
Punto en Y = 40 + 4π/3π = 4(25mm)/3(3.1416) = 10.61 mm = 50.61 mm


Area de Rectangulo:
B x H = 50mm * 40 mm = 2000 mm^2

Punto en X = 25 mm
Punto en y = 20 mm

Cuadrado area:

L x L = 20mm * 20mm = 400 mm^2

Punto en X = 60 mm
Punto en y = 10 mm

CENTROIDE EN LA COORDENADA X :

X= ((A1)(X1)+(A2)(X2)+(A3)(X3) )/ Atotal

X= (981.74mm^2)(25mm) + (2000mm^2)(25)+(400mm^2)(60) / 3381.74 mm

X= 29.13 mm

CENTROIDE EN LA COORDENADA Y:

Y = (A1)(Y1)+ (A2)(Y2) + (A3)(Y3) / Atotal

Y = (981.74mm^2)(50.61mm) + (2000mm^2)(20mm) + (400mm^2)(10) / 3381.74 mm

Y = 27.70 mm


Pasando las coordenadas a Cm

Coordenada en X = 2.91cm
Coordenada en Y = 2.77cm

Esta es la Respuesta corrrecta xq no habia tomado en cuenta la coordenada del cuadrado de despues de la pieza q es compuesta gracias solo fue una pequeña correccion